R Squared

Introduction

This is all about R².

My Thoughts

Least Squares Review

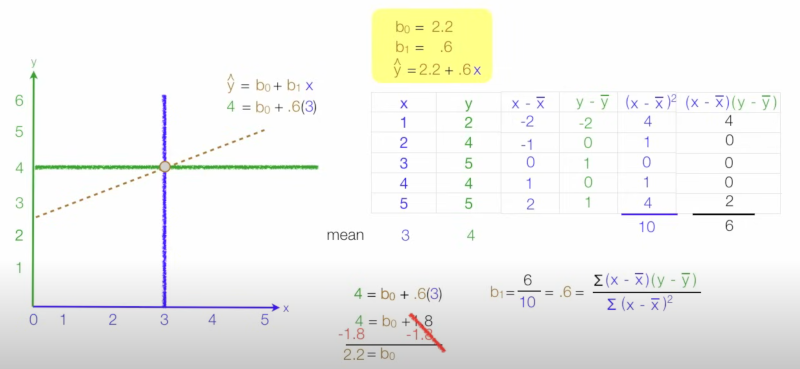
Most of this requires you to think about a dataset with lots of points. What we are trying to do is with least squares is find the best fit for a line for our data points. Once we have this we could maybe predict for a new data point what the y-value might be given the x-value. Here is the formula
$S=\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$
And here is an example of usage

R Squared

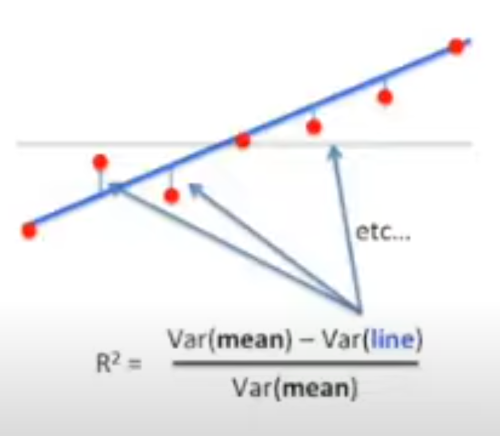
With $R^2$ we are looking at the variances (changes) using the mean and the line. Squaring means we don't care about negative or positive.

What is the difference

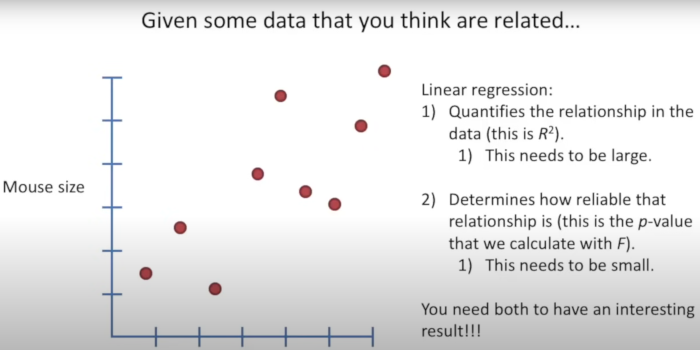
Well I guess R² = R squared. R² is the variance between a dependent variable and an independent variable in terms of percentage. Therefore 0.4 R² = 40% and R = 0.2. I guess I agree that using R² does provide an easier way to understand what you mean however there is no sign on R².

Formula for R²

This is given by

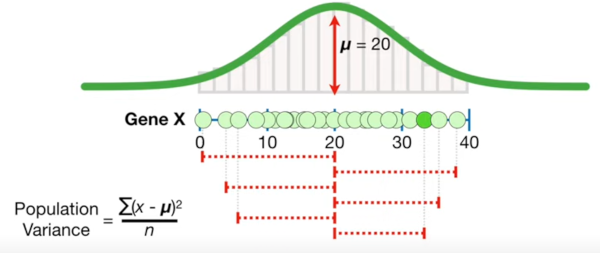
A reminder of how we calculate variance, we add up the differences from the mean like below. Note this shows a population and we should divide by n-1 not n but I liked the graphic.

This was a nice picture

F

Spent a lot of time looking a this but got nowhere. It is a way to get a p-value. For F the following formula we given.

The Pfit and Pmean explanations were provided. Pfit was the number of parameters. E.g. for mouse we could look at weight, size and tail. And the Pmean was the number of means, which is normally 1. The n is the number not explained by the fit. This took a while but I believe this to be the residuals Observed (y) - Predicted (y_hat).