Calculus: Difference between revisions
Created page with "=Introduction= This is my page on Calculus hopefully reminding me of my earlier youth =Limits= This is where you are given and equation and you have to specify the limit. The approach to solving these is *Substitute the value asked for *Multiply the top to cancel the bottom *Multiply by the conjugate, this is where we take and expression with a real and imaginary part and flip the signs.So the x -3 has a real value of x and an imaginary value of -3.<br> File:Conjugate1..." |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
This is my page on Calculus hopefully reminding me of my earlier youth | This is my page on Calculus hopefully reminding me of my earlier youth | ||
=Limits= | =Limits= | ||
==Intro== | |||
This is where you are given and equation and you have to specify the limit. The approach to solving these is | This is where you are given and equation and you have to specify the limit. The approach to solving these is | ||
*Substitute the value asked for | *Substitute the value asked for | ||
| Line 9: | Line 10: | ||
We an multiply the top and the bottom by the conjugate<br> | We an multiply the top and the bottom by the conjugate<br> | ||
[[File:Conjugate2.png]]<br> | [[File:Conjugate2.png]]<br> | ||
And then the answer is 1/6<br> | |||
[[File:Conjugate3.png]]<br> | |||
==Graphs== | |||
Limit on graph are simple, you take the measurement from the left, the measurement from the right and if they are the same you are good to go.<br> | |||
[[File:Limits graph1.png]]<br> | |||
If they don't match then DNE (Does not exist) is the answer<br> | |||
[[File:Limits graph2.png]]<br> | |||
Where the answer is infinity because the substitution is over 0. This produces the red line, a vertical asymptote. On the graph we can see at -3 on the x-axis the graph does not join up. This is a '''jump discontinuity''' and is not removable. At -2 we have '''hole''' which is a '''removable discontinuity'''. | |||
Latest revision as of 03:09, 1 May 2025
Introduction
This is my page on Calculus hopefully reminding me of my earlier youth
Limits
Intro
This is where you are given and equation and you have to specify the limit. The approach to solving these is
- Substitute the value asked for
- Multiply the top to cancel the bottom
- Multiply by the conjugate, this is where we take and expression with a real and imaginary part and flip the signs.So the x -3 has a real value of x and an imaginary value of -3.
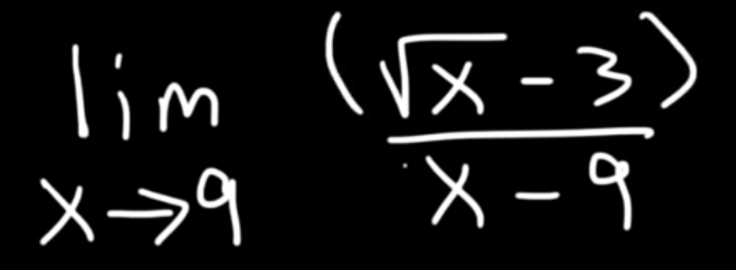
We an multiply the top and the bottom by the conjugate

And then the answer is 1/6
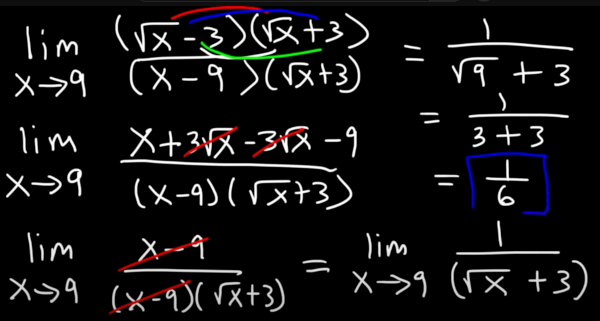
Graphs
Limit on graph are simple, you take the measurement from the left, the measurement from the right and if they are the same you are good to go.
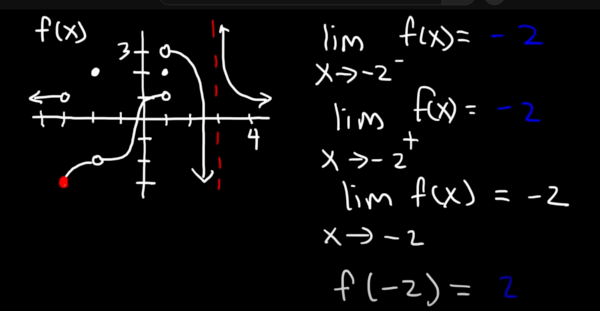
If they don't match then DNE (Does not exist) is the answer
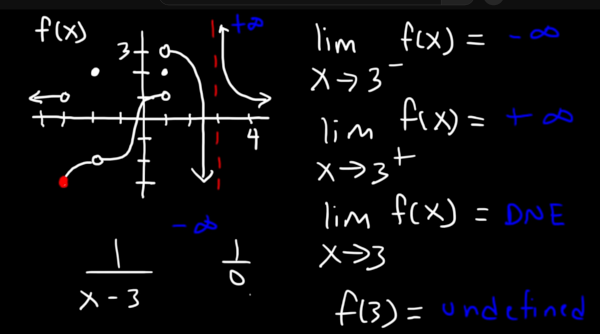
Where the answer is infinity because the substitution is over 0. This produces the red line, a vertical asymptote. On the graph we can see at -3 on the x-axis the graph does not join up. This is a jump discontinuity and is not removable. At -2 we have hole which is a removable discontinuity.