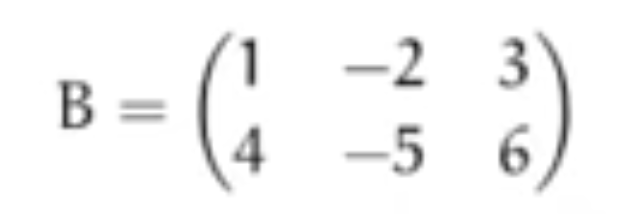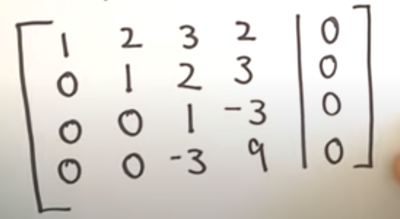Matrices and Vectors: Difference between revisions
| Line 10: | Line 10: | ||
And here are the linear equations using gaussian and vectors | And here are the linear equations using gaussian and vectors | ||
[[File:Vector gaussin.png|600px]]<br> | [[File:Vector gaussin.png|600px]]<br> | ||
= | =Homegenous Systems= | ||
Homegenous Systems always has a least one solution. Watching an alternative video showed the questions using the form 2x₁ + 4x₂ rather than 2a + 4b. There are two types of Homegenous Systems, trivial and non-trivial. The trivial solution is where all the variables are = to zero. This demonstration helped a lot in how to solve this. Here was the question<br> | |||
[[File:Nt 1.png]]<br> | |||
We write this down by writing the coefficients.<br> | |||
[[File:Nt 2.png]]<br> | |||
We are looking to get a zero in column 0 so we doing the following | |||
-1R₁ + R₂ => R₂ | |||
-2R₁ + R₃ => R₃ | |||
R₁ + R₄ => R₄ | |||
[[File:Nt 3.png]]<br> | |||
In the above the notation separates out the constants and the two variables and their coefficients. This is referred to as | In the above the notation separates out the constants and the two variables and their coefficients. This is referred to as | ||
General = Particular + Homegenous | General = Particular + Homegenous | ||
Revision as of 02:32, 21 January 2025
Introduction
Next as the title says
Example
Vector Operations
We can add the components or scale them provided they are the same size

Gaussian as Vectors
And here are the linear equations using gaussian and vectors

Homegenous Systems
Homegenous Systems always has a least one solution. Watching an alternative video showed the questions using the form 2x₁ + 4x₂ rather than 2a + 4b. There are two types of Homegenous Systems, trivial and non-trivial. The trivial solution is where all the variables are = to zero. This demonstration helped a lot in how to solve this. Here was the question
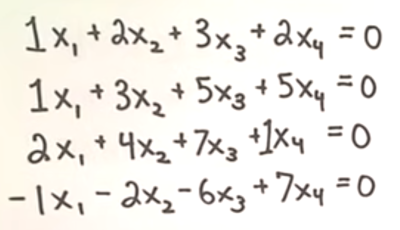
We write this down by writing the coefficients.
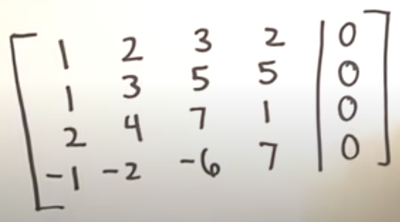
We are looking to get a zero in column 0 so we doing the following
-1R₁ + R₂ => R₂ -2R₁ + R₃ => R₃ R₁ + R₄ => R₄
In the above the notation separates out the constants and the two variables and their coefficients. This is referred to as
General = Particular + Homegenous
= Constants + Coefficients
Terms
- m x n a matrix of m row, n colums
- Capital let for name of Matrix
- Small letter for entry