Electronic Formulas Page

Ohms Law

Ohm’s law states that the voltage across a conductor is directly proportional to the current flowing through it, provided all physical conditions and temperatures remain constant.

To demonstrate this a demo circuit was set up.

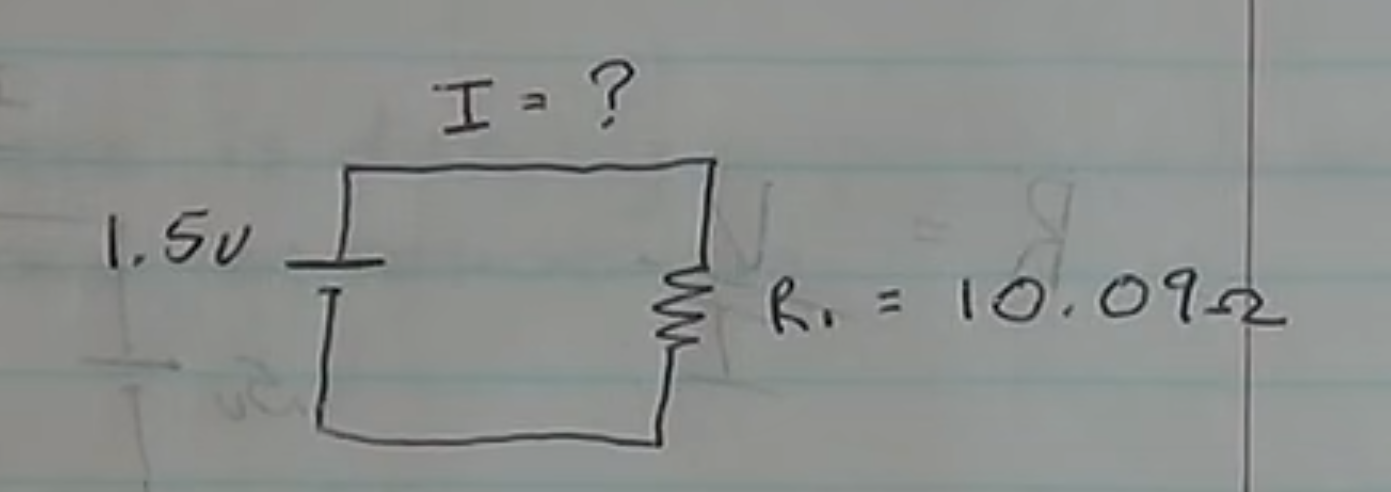
The circuit is put together and given the values the expected result is

1.5v ÷ 10.09Ω = 0.148A or 148mA

A you can see the answer was not as expected but instead 104.43mA. The reason for this is that the circuit has additional resistance due to the multi-meters.

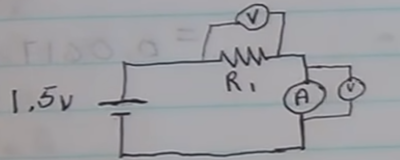
Luckily we are measuring these values

Looking a first measurement over the resistor

R₁ = V/I
= 1.05v ÷ 0.104A = 10.09Ω

Looking a second measurement over the multi-meter

Rₐ = V/I
= 0.21v ÷ 0.104A = 2.02Ω

Total Resistance calculated by adding together because we are in series

Rₜ = V/I
= 10.09Ω + 2.02Ω = 12.11Ω

Calculating the Total Amps

Amps = V/I
= 1.5 ÷ 12.11Ω = 0.123A or 123mA

Now lets calculate the Total Resistance using actual current meter reading (0.104A) and the (1.5) voltage.

R"ₜ" = V/I
     = 1.5v / 0.104A = 14.4Ω

Given we now know the actual resistance and the total resistance gives to the wiring resistance.

= 14.4Ω (calculated from the meter reading and the input voltage) - 12.11Ω (Calculated from total resistance) = 2.29Ω