Verilog Language

Introduction

This page is meant to help understand how to approach the language. There are three levels of abstraction.

Way to describe Hardware

• Gate Level
• Dataflow Level
• Behavioral Level

Types of Logic

• Combinational Logic
• Sequential Logic

Combinational Logic

This is where the outputs are a simple function of the inputs. (Sounds like pure functions

2 to 1 Multiplexer using Combinational

This example shows the 3 approaches we can use to describe the hardware

Gate Level

This was quite useful as I have some knowledge of gates and boolean logic so it starts to make a bit of sense in verilog. Here is the truth table for the 2 to 1 multiplexer

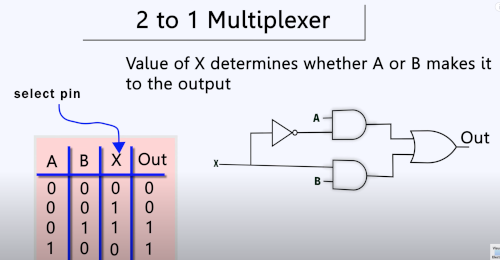
To model this at the gate level we could do this

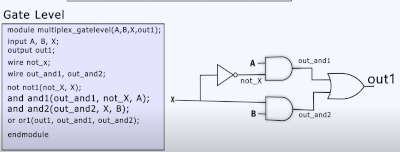
So this is what I learned to get to the answer shown. To solve the problem you name all of the gates, it maybe you name based on type of gate and increment, e.g. and1, and2, and3. These are not shown in the diagram, instead what is named are the wire connecting the gates. These wires need to be declared.

wire not_x;
wire out_and1;
wire out_and2;

• not gate = not1
• and gate (top) = and1
• and gate (bottom) = and2
• or gate = or1

Now to model these we write down the appropriate type, the name, the output, followed by the input so.

• not_x = not not1(not_x, X)
• and1 = and and1(out_and1, A, not_x)
• and2 = and and2(out_and2, X, B)
• out1 = or or1(out1, out_and1, out_and2)

Dataflow Level

And now the Dataflow level. This does look a lot like boolen logic and is very unreadable.

Behavioral Level

Finally the Behavioral Level which does seem more in my wheel house. The code uses a procedure block where the code only executes when there is a change in the signal

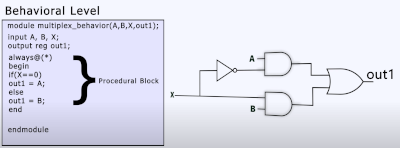
Sequential Logic

Sequential logic uses memory and state. It uses combinational logic too.

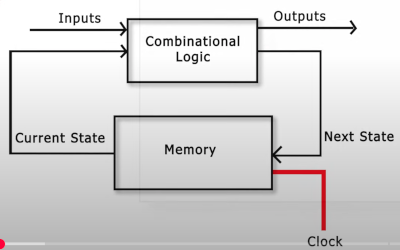
A bit more complex and a bit of memory required on my part.
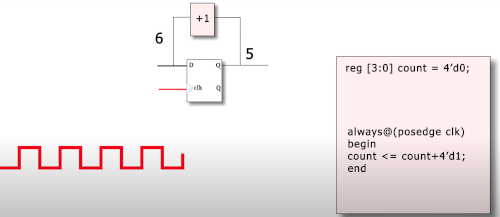
This diagram shows a d-flip flop where the input is the same as the output on a rising edge. The code only executes on a positive edge. It uses a non bloicking assignment <=

Revisiting the Adder

This is when I now understand hopefully how to model gates

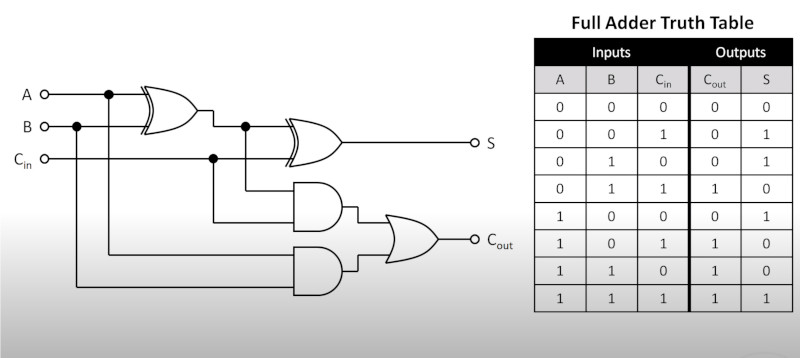
Given this knowledge I

• label the gates
• label the outputs

Which gives this picture

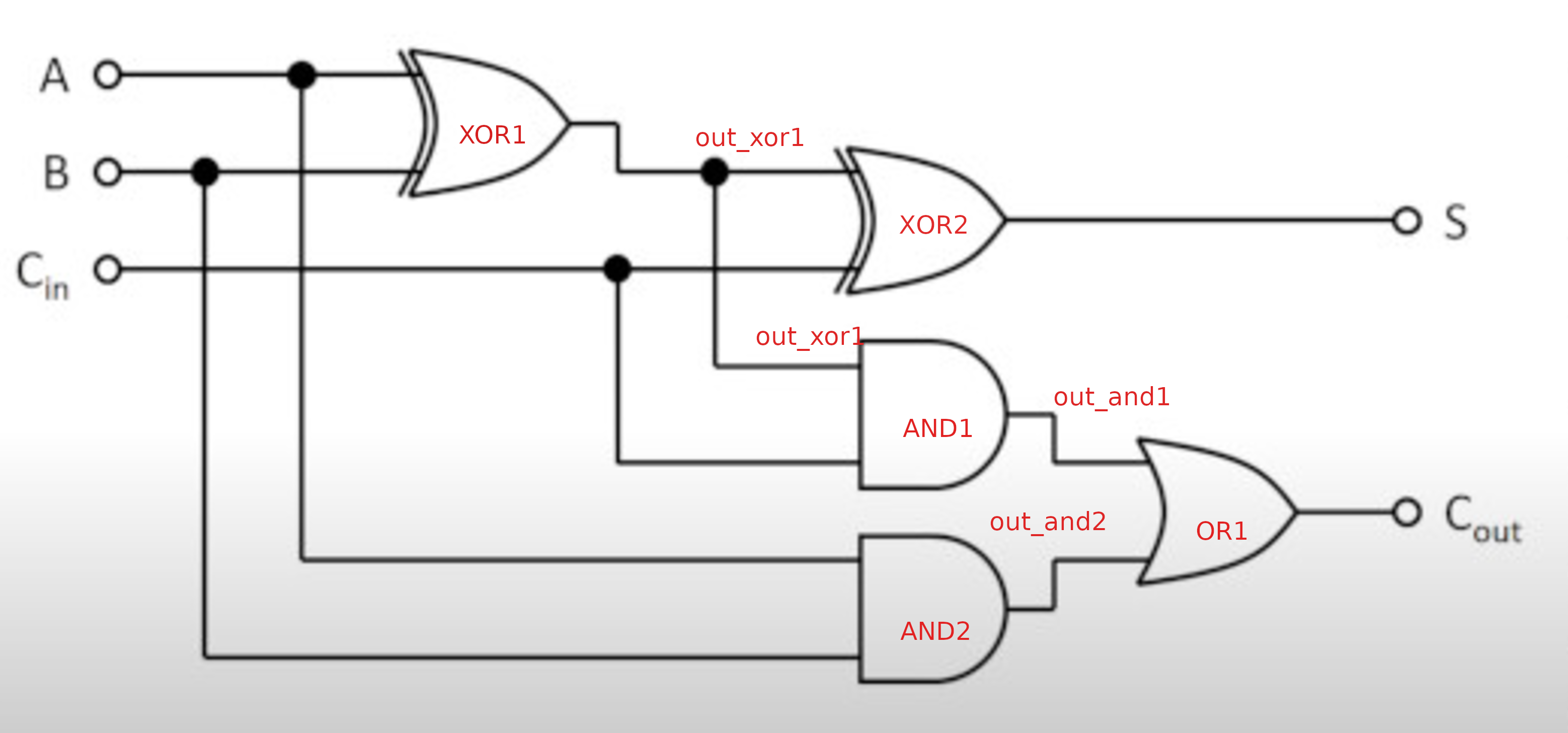
Now we can write the verilog for this using the approach above

module main(
    input A,
    input B,
    input Cin,

    output Cout,
    output S
);
    wire out_xor1;
    wire out_xor2;
    wire out_and1;
    wire out_and2;

    xor XOR1(out_xor1, A, B);
    xor XOR2(S, out_xor1, Cin);
    and AND1(out_and1, out_xor1, Cin);
    and AND2(out_and2, A, B);
    or  OR1(Cout, out_and1, out_and2);
endmodule

On the other page I used boolean logic to implement this. We started with this

S    = (A̅.B̅.C ) +  (A̅.B.C̅) + (A.B̅.C̅) + (A.B.C)
Cₒᵤₜ = (A̅.B.C ) +  (A.B̅.C) + (A.B.C̅) + (A.B.C̅)

And ended with

Cₒᵤₜ = C (A̅ ⊕ B̅) + AB
S    = C ⊕ A ⊕ B 

module main(
    input A,
    input B,
    input Cin,

    output Cout,
    output S
);
    // Cout
    assign Cout = (Cin & (!A ^ !B) ) | (A & B);

    // S
    assign S = Cin ^ A ^ B;
   
endmodule

Language Quick Reference

Here is a quick reference File:Verilog Quick Reference Card v2 0.pdf