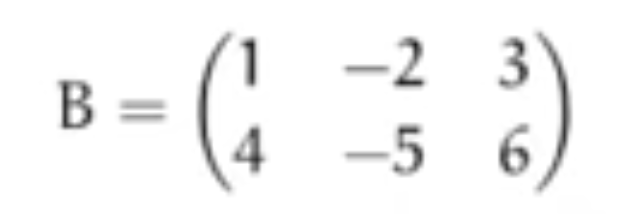Matrices and Vectors

Introduction

Next as the title says

Example

Here we go

Vector Operations

We can add the components or scale them provided they are the same size

Gaussian as Vectors

And here are the linear equations using gaussian and vectors

Notation

In the above the notation separates out the constants and the two variables and their coefficients. This is referred to as

General = Particular + Homegenous
        = Constants + Coefficients

Terms

• m x n a matrix of m row, n colums
• Capital let for name of Matrix
• Small letter for entry