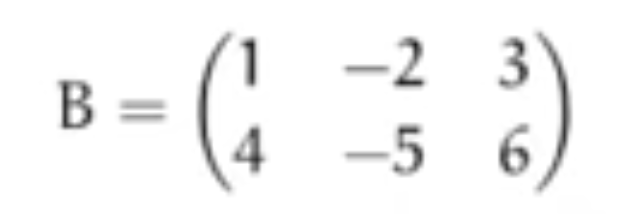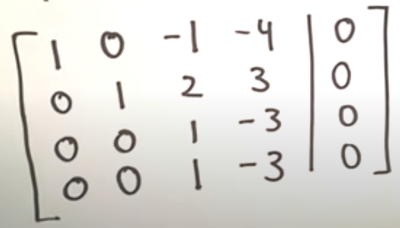Matrices and Vectors

Introduction

Next as the title says

Example

Here we go

Vector Operations

We can add the components or scale them provided they are the same size

Gaussian as Vectors

And here are the linear equations using gaussian and vectors

Homegenous Systems

Homegenous Systems always has a least one solution. Watching an alternative video showed the questions using the form 2x₁ + 4x₂ rather than 2a + 4b. There are two types of Homegenous Systems, trivial and non-trivial. The trivial solution is where all the variables are = to zero. This demonstration helped a lot in how to solve this. Here was the question

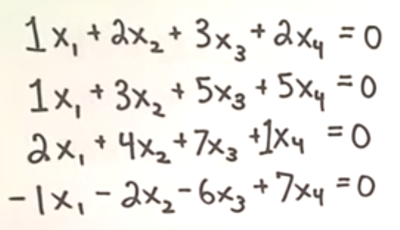
We write this down by writing the coefficients.

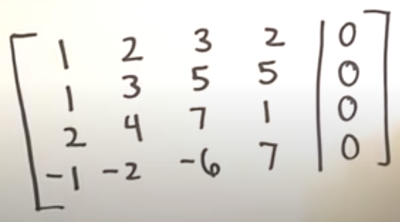
We are looking to get a zero in column 0 so we doing the following

-1R₁ + R₂ => R₂
-2R₁ + R₃ => R₃
  R₁ + R₄ => R₄

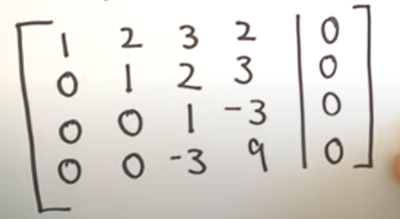
Next step we do the following a 3 is a multiple of 4

  1/3R₄ => R₄

In the above the notation separates out the constants and the two variables and their coefficients. This is referred to as

General = Particular + Homegenous
        = Constants + Coefficients

Terms

• m x n a matrix of m row, n colums
• Capital let for name of Matrix
• Small letter for entry