Haskell

Introduction

This is my first dip into Haskell, just felt like trying it. Haskell is a purely functional programming language. rather than a declarative language. I.E. it is a declarative language rather than imperative. With declarative, you tell the language what the thing is rather than how to do the thing.

Features

Lazy

Haskell is a programming lazy language and only evaluates on usage. E.g. only evaluates the first 10

let infiniteList =  [1..]
take 10 infiniteList

Modules

Starting to look a lot like Lisp. This next bit shows how you can combine various functions of your own to produce and output

let double = x = x * 2
let increment x = x + 1
let doubleThenIncrement x = increment(double x)
doubleThenIncrement 10 -- Answer is 21

Statically Typed

With Haskell types are inferred

Hello World

Here we start with main and strange format but no curly brackets which is good.

main :: IO()
main = putStrLn "Hello World"

We build like gcc using

ghc hello.hs -o hello

Types

• Int, Integer e.g. 1
• Float, Double 21.3
• Chars e.g. 'S'
• Boolean e.g. True, False
• List e.g. [1,2,3], [True, False, True], elements must be of same type
• Tuple e.g. (1,2,3, "string, True)

Function Signature

With Haskell there are no variables as things are immutable. Therefore what look list variable declarations are actually more like consts and call definitions e.g.

name:: String
name = "Bob"

For functions with one argument this is straight forward

square :: Int -> Int
square v =v * v

But more arguments not a straight forward and seem to be declared like currying functions. Remember the last type is the result of the function

product :: Int -> Int -> Int
product x y  = x * y

We can have a signature with no specific type. Haskell handles these polymorphic types

first :: (a,  b) -> a
first (x, y) = x

The function must return value of type of a.

Notation

Not complicated just how the format operators

Prefix

We use the operator before the arguments. Note brackets around symbol operator

(+) 3 4
prod 3 4

Infix

We use the operator between the arguments. Note for non symbol, need back ticks

3 + 4
3 `prod` 5

Lists

We can assess lists using the double bang operator. e.g.

"abc" !! 1 -- b 
[12,13, 16,18] !! 3 -- 18

-- Make a list
[3..5] -- [3,4,5]

-- Make a list with step
[3,5..13] -- [5,8,12]

-- Make an infinite list
[5..]

-- Take 
take 3 [1,2,3,4] -- [1,2,3]

-- Concat with ++
[1,2] ++ [3,4] -- [1,2,3,4]
 
-- Make a list with letters
['a', 'c'...'f'] -- ["acdef"]

-- Null Length, sum and `elem`

Here are some more examples

let x = [1..10]
head x -- 1
tail x -- [2,3,4,5,6,7,8,9,10]
last x -- 10
init x -- [1,2,3,4,5,6,7,8,9]
reverse x -- [10,9,8,7,6,5,4,3,2,1]
length x -- 10
take 5 (x) -- [1,2,3,4,5]
drop 6 (x) -- [7,8,9,10] 
sum x -- 55
product x -- 3628800
elem 8(x) -- True Searches list
null x --- False

We also have words, unwords, lines and unlines to join and break text

Conditionals

If else

You must use the else as every function must return a value

main = do   
   let var = 23 
   if var `rem` 2 == 0 
      then putStrLn "Number is Even" 
   else putStrLn "Number is Odd"

Guards

Simple and easy to read

bookCategory :: Int -> String
bookCategory age
    | age < 10 = "Children's book"
    | age < 18 = "Teen book"
    | otherwise = "Adult book"

main = do
    print(bookCategory 5)
    print(bookCategory 15)
    print(bookCategory 25)

Pattern Matching

Again easy pezzy and I love pattern matching

-- Pattern Matching
coffeeType :: String -> String
coffeeType "Epresso" = "Strong and bold"
coffeeType "Cappuccino" = "Frothy and delicious"
coffeeType "Filter" = "Watery and weak"
coffeeType _ = "I have no idea what that is"

main = do 
    print(coffeeType "Epresso")
    print(coffeeType "Cappuccino")
    print(coffeeType "Filter")
    print(coffeeType "Latte")

Case Expressions

Again easy pezzy

checkForZeroes :: (Int, Int,Int) -> String
checkForZeroes (0,_,_) = "First is zero"
checkForZeroes (_,0,_) = "Second is zero"
checkForZeroes (_,_,0) = "Third is zero"
checkForZeroes _ = "No zeros"

checkForZeroes(32,0,256) -- "Second is zero"

Let expressions

The word bind haughts me, it is like trying to remember Samuel L Jackson's name. Here is the tutors opening gambit
With in

func arg = 
  let <BIND_1>
      <BIND_2>
  in <EXPR that uses BIND_1 and/or BIND_2>

With where

func arg = <EXPR that uses BIND_1 and/or BIND_2>
  where <BIND_1>
        <BIND_2>

I have to say they are now speaking my language as this was the example which does look pretty pretty awful

hotterInKelvin :: Double -> Double -> Double
hotterInKelvin c f = if c > (f- 32) * 5/9 then c + 273.16 else (f - 32) * 5/9 + 273.16
hotterInKelvin 40 100 -- 273.16

Now we have this and I understand the BIND_1 or BIND_2 are just declared expressions for use with the in control

hotterInKelvin2 :: Double -> Double -> Double
hotterInKelvin2 c f = 
    let fToCelius t = (t - 32) * 5 / 9
        cToKelvin t = t + 273.16
        fToKelvin t = cToKelvin (fToCelius t)
    in if c > fToCelius f then cToKelvin c else fToKelvin f

And using where approach

hotterInKelvin3 :: Double -> Double -> Double
hotterInKelvin3 c f = 
    if c > fToCelius f then cToKelvin c else fToKelvin f
    where
        fToCelius t = (t - 32) * 5 / 9
        cToKelvin t = t + 273.16
        fToKelvin t = cToKelvin (fToCelius t)

I prefer the where one because I can stop reading quicker but they said I would take time to workout and sometimes preference

More on Functions

High Order functions

Now I know more about signature and how to read them

applyTwice :: (a->a) -> a -> a
applyTwice f x = f (f x)

Make must more sense, as the signature shows

• the first argument is a function take a type a and returning a type a,
• the second a value of type a and
• the result is of type a

Built-in Map function

let increment x = x + 1
map increment [1,2,3] -- [2,3,4]

Built-in Filter function

And filter, loving the mod operation

let isEven n = n `mod` 2 == 0
filter isEven [2,3,4] -- [2,4]

Built-in Foldl function

Finally something new, foldl, i.e. apply operation start from position using array from left to right (lispy)

foldl (+) 0 [1,2,3,4,5] -- 15

Sort function and others

And now first use of libraries

import Data.List (sort)
sort [10, 2, 5, 3, 6, 7, 4, 8, 9, 1]

Other functions were zipWith, takeWhile, dropWhile

-- All
all even [1,2,4] -- False
any even [1,2,4] -- True

Lambda Expressions

This is a shortcut to writing unnamed function. We do this by

• specifying a back slash
• specifying arguments
• an arrow
• specifying body

print((\c -> c * 9/5 + 32) 25) -- 77.0

Precedence and Associativity

In Haskell the operators have a precedence, like looking at type with :t you can see this with :i (+). The higher the number the higher the precedence. If two have the same then then the associativity decides. So for (+) the :i shows infixl (i.e. left)

Curried Functions

All functions take on argument in Haskell. Hopefully this explains it as all functions are broken down and applied

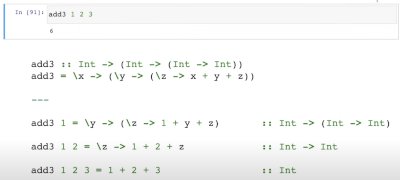
Function application $ Operator

Gosh tired and messed with my brain but I think it means a $ will usually put parentheses around the arguments following

(2 *) 3 + 4 -- ((2 *) 3) + 4     = 10
(2 *) $ 3 + 4 -- (2 *) (3 + 4)   = 14

max 5 4 + 2   -- ((max 5) 4) + 2   = 7
max 5 $ 4 + 2 -- (max 5) (4 + 2)  = 6

The biggest use of $ is to replace a set of parentheses to make code more readable

show ((2**) (max 3 (2 + 2)))  -- 16
show $ (2**) (max 3 (2 + 2))  -- 16
show $ (2**) $ max 3 (2 + 2)  -- 16
show $ (2**) $ max 3 $ 2 + 2  -- 16

Recursion

Where would we be without Factorial

-- Factorial
factorial :: Int -> Int
-- Base case
factorial 0 = 1
-- Recursive case
factorial n = n * factorial (n - 1)

main = do
    print(factorial 5)

Modules

Modules are, as ever, just functionality you can import. We looked at Data.List

main = do
  print(intersperse '|' "ILoveHaskell") -- I|L|o|v|e|H|a|s|k|e|l|l
  print(intercalate ' ' ["Haskell", "is", "great"]) -- "Haskell is great"
  print(splitAt 3 "Apple") -- ("App","le")

And the Data.Char module.

main = do
  print(toUpper 'a') -- A
  print(toLower 'B' -- b
  print(words 'FRED WAS') -- ["FRED", "WAS"]

And the Data.Map. The importing of this seemed to be a bit blurry even to the tutor

import Data.Map (Map)
import qualified Data.Map as Map

myMap :: Integer -> Map Integer [Integer ]

myMap n = Map.fromList (map makePair [1..n])
  where makePair x = (x, [x])

main = do
  print $ myMap 10

And the Data.Set

main = do
  print $ Set.fromList "Hey Jude!" -- " !HJdeuy"

Roll your Own

This seem a little hairy to recompile and make sure we are running the correct code. Possibly need to look at the tools for this

module Custom(
    showEven,
    showOdd
) where 
  showEven :: Int -> String
  showEven x = if x `mod` 2 == 0 then "Even" else "Odd"

  showOdd :: Int -> String
  showOdd x = if x `mod` 2 == 0 then "Odd" else "Even"

File IO

Reading

Very easy

main = do
    contents <- readFile "movies.txt"
    putStr contents

Writing

main = do
    let movies = ["The Godfather", "The Shawshank Redemption", "The Dark Knight", "Pulp Fiction", "The Lord of the Rings: The Return of the King"]
    writeFile "movies.txt" (unlines movies)
    putStrLn "Movies written to movies.txt"

Exception Handling

Here is an example of catching a division by zero in Haskell

import Control.Exception

main = do
  result <- try (evaluate (div 5 0)) :: IO (Either SomeException Int)
  case result of
    Left ex -> putStrLn $ "Caught exception: " ++ show ex
    Right val -> putStrLn $ "The result was: " ++ show val

Functors

Introduction

The definition I got from C++ is function object is a function with state.

Simple C++ Example

struct Value {
   int m_result {0};
   
   int operator()(int newResult) {
       m_result = newResult;
       return m_result;
   }
}

int main() {
  Value v;
  v(42);
  std::cout << v.m_result << std::endl;
}

Better C++ Example

They went on to provide a second C++ example where the Comparator was used as a good use of a functor. Calling the function Comparator with the state of the goblins.

struct Goblin {
    int health;
    int strength;
    Goblin(int health, int strength) : health(health), strength(strength) {};

    bool operator<(const Goblin& other) const {
        return health < other.health;
    }
};

struct GoblinComparator {
    bool operator()(const Goblin& a, const Goblin& b) const {
        return a.strength < b.strength;
    }
};

int main() {
    std::vector<Goblin> goblins {
        {5, 25},
        {3, 25},
        {100, 1}
    };

    std::sort(goblins.begin(), goblins.end(), GoblinComparator());

    for(const auto& goblin : goblins) {
        std::cout << "Health: " << goblin.health << " Strength: " << goblin.strength << std::endl;
    }

    return 0;
}

// Health: 100 Strength: 1
// Health: 5 Strength: 25
// Health: 3 Strength: 25

Much Better Example

Googling to make sure I understood the idea of a functor, found a much better example. which was a logger and all makes sense now.

class Logger {
public:
    Logger(const std::string& fileName) {
        m_output.exceptions(m_output.badbit | m_output.failbit);
        try
        {
            m_output.open(fileName, std::ofstream::out);
            m_output << "Logger started" << std::endl;
        }
        catch (const std::ofstream::failure& e)
        {
            std::cerr << "Failure: " << e.what() << std::endl;
            std::string error = "Could not open file: " + fileName;
            std::cout << error << std::endl;
            throw std::runtime_error(error);
        }

    }

    void operator() (const std::string& message) {
        m_output << message << std::endl;
    }

    public:
    ~Logger() {
        m_output.flush();
        m_output.close();
    }

private:
    std::ofstream m_output;
};

int main() {
    Logger logger("log.txt");
    logger("Hello, world!");
    return 0;
}

Back to Haskell

Arggghhhhh

To I am still struggling but this is what the definition of a functor is and therefore some kind of type definition, i.e. anything which looks like this is a functor

class Functor f where
    fmap :: (a->b) -> f a -> f b

The fmap definition is I guess

(a->b) -> f a -> f b

This was explained as
fmap takes a function which is of type a and results in a type b
It applies f of a and gives you a f of b

Map and FMap

So some progress, the tutor showed a couple of things which start to make more sense in the interactive session. They the types which I knew but here to keep context

:t False -- Bool
:t "hello" -- String
:t 'T' -- Char
:t 12  -- Num a=>a (an instance of typeclass Num not type)
-- Now lets look at our Maybe (like Option but instead on Some and None, Just and Nothing)
:t Nothing -- Maybe a
:t Just 5 -- Num a => Maybe a

It is the last one where thing are starting to make sense, the output suggests you put a in and you get a out. So we can now use the kind or k to look a the type constructors

:k Bool -- :: *
:k String -- :: *
:k Char -- :: *
:k Int -- :: *
-- Now lets look at our Maybe
:k Maybe -- * -> * Which means it is a function converting from type to type

So looking a map

-- Example
map (+2) [1,2,3] -- [3,4,5]

-- Looking at type
:t map -- map :: (a -> b) -> [a] -> [b]

This looks a lot like the type of fmap. fmap came first but because lists are so useful they made a specific implementation of fmap called map for lists.
You can use fmap for any shape of data but you have to tell it how to traverse the data you are using. In the example you talked about trees.

Third Video

So opening line was great, a functor is a TYPECLASS. A typeclass, you can think of as an interface you need to implement.

class Functor f where
    fmap :: (a->b) -> f a -> f b

As Oliver Hardy might say, now we are getting somewhere. The video went on to distinguish between types where are wrapped and unwrapped. They eluded to the Maybe type which can be a Just or Nothing. They demonstrated unwrapped values can be evaluated

 
(+3) 9 -- 12 Where 9 is unwrapped
-- but
(+3) (Just 9) -- Will not work

Now the Functor for some types are already defined including, Maybe, Either and List so to demonstrate we can make our on type, a copy of Maybe using this

 
data Maybe2 a = Just2 a | Nothing2 deriving Show

Now we can make our own Functor for Maybe2

 
instance Functor Maybe2 where 
    fmap func (Just2 a) = Just2 (func a)
    fmap func Nothing2 = Nothing2

Putting it together we have

 
import Data.Functor

data Maybe2 a = Just2 a | Nothing2 deriving Show

instance Functor Maybe2 where
  fmap f (Just2 x) = Just2 (f x)
  fmap f Nothing2 = Nothing2

main = do
    print $ fmap (+1) (Just2 10) -- Just2 11
    print $ fmap (+2) (Nothing2) -- Nothing2

Trees

Now we come on to the tree, the most common example I have seen. For fmap and a tree we want to apply a function at the tip of the branch to get everything. This will involved recursion as a branch can have many branches

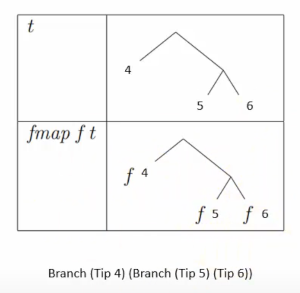
So here is a C# Recursive approach before we start

 
    // Function to perform inorder traversal
    static void inorderTraversal(Node node) {
      
        // Base case
        if (node == null)
            return;

        // Recur on the left subtree
        inorderTraversal(node.left);
      
        // Visit the current node
        Console.Write(node.data + " ");
      
        // Recur on the right subtree
        inorderTraversal(node.right);
    }

But with Haskell this does seem somewhat more readable

 
import Data.Functor

data Tree a = Tip a | Branch (Tree a) (Tree a) deriving Show

instance Functor Tree where
  fmap f (Tip x) = Tip (f x)
  fmap f (Branch left right) = Branch (fmap f left) (fmap f right)

x = Branch (Tip 4) (Branch (Tip 5) (Tip 6))

main = do
    print $ fmap (*2) x

Finally

Whilst I understood functor for both C++ and Haskell, I did not understand how a C++ functor related to a Haskell one too much. Time means I march on to Monads

Applicative

Introduction

When they say applicative, they are referring to the <*> symbol. Now we use applicatives they always have a defined Functor, this has the following TypeClass definition

class Functor => Applicative f where
    pure :: a-> f a
    (<*> :: f (a ->b) -> f a -> f b

You will notice that the second clause is exactly the same as Functor aside from the f

Example 1

Here is an example of using the applicative

import Data.Functor

data Maybe2 a = Just2 a | Nothing2 deriving Show

instance Functor Maybe2 where
  fmap f (Just2 x) = Just2 (f x)
  fmap f Nothing2 = Nothing2

instance Applicative Maybe2 where
  pure = Just2
  Just2 f <*> Just2 x = Just2 (f x)
  -- _ <*> _ = Nothing2

main = do
    print $ fmap (+1) (Just2 10)
    print $ fmap (+2) (Nothing2)
    print $ Just2 (+3) <*> Just2 10 -- Just2 13

Example 2

Its time for the tree again

 
import Data.Functor

data Tree a = Tip a | Branch (Tree a) (Tree a) deriving Show

instance Functor Tree where
  fmap f (Tip x) = Tip (f x)
  fmap f (Branch left right) = Branch (fmap f left) (fmap f right)

instance Applicative Tree where
  pure x = Tip x
  Tip f <*> x = fmap f x
  Branch left right <*> x = Branch (left <*> x) (right <*> x)

x = Branch (Tip 4) (Branch (Tip 5) (Tip 6))

main = do
    print $ Tip (*4) <*> x -- Branch (Tip 16) (Branch (Tip 20) (Tip 24))
    print $ Branch (Tip (+1)) (Tip (*2)) <*> x -- Branch (Branch (Tip 5) (Branch (Tip 6) (Tip 7))) (Branch (Tip 8) (Branch (Tip 10) (Tip 12)))

Monads

So this is the Monad bit which I what I started on to learn this. Like Functors, the explanation may have been written in greek. I have no idea what he meant

class Monad m where
    return :: a -> m a
    -- Bind
    (>>=) :: m a -> (a -> m b) -> m b
    -- Then
    (>>) :: m a -> m b -> m b 
    x >> y = x >>= \_ -> y
    -- Fail
    fail :: String => m a
    fail msg = error msg

He preceded to speak about 3 laws of Monads

--- Three Laws of Monads:

--- 1 Left Identity:
return a >> = f
--- the same as : f a

-- 2 Right identity:
x >>= return
-- the same as: x  {Value not changed}


-- 3 Associativity:
(m >>= f) >>= g
m >>= (\x -> f x >>=g)

Moniods

The explanation was again useable. This is left here to fill in later