R Squared: Difference between revisions
| Line 13: | Line 13: | ||
((a*x_1 + b) - y_1)^2 + (a*x_2 + y_2)^2 + | ((a*x_1 + b) - y_1)^2 + (a*x_2 + y_2)^2 + | ||
</math>... | </math>... | ||
<br> | |||
And here is an example of usage<br> | |||
[[File:Lsq9.png|600px]]<br> | |||
=What is the difference= | =What is the difference= | ||
Revision as of 02:00, 23 April 2025
Introduction
This is all about R².
My Thoughts
Least Squares Review
Most of this requires you to think about a dataset with lots of points. What we are trying to do is with least squares is find the best fit for a line for our data points. Once we have this we could maybe predict for a new data point what the y-value might be given the x-value. Here is the formula
Or in english we have
...
And here is an example of usage
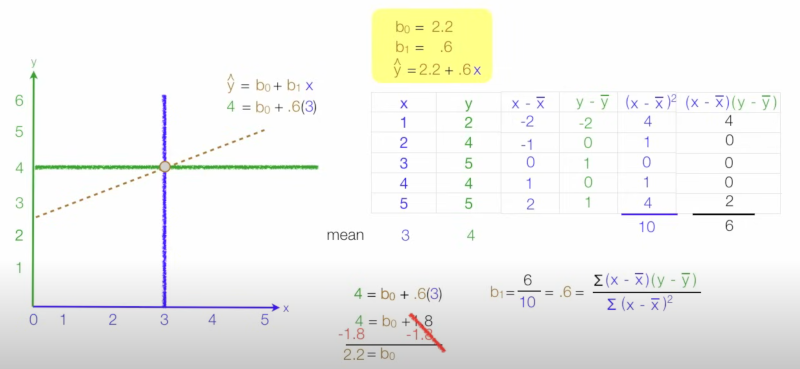
What is the difference
Well I guess R² = R squared. R² is the variance between a dependent variable and an independent variable in terms of percentage. Therefore 0.4 R² = 40% and R = 0.2. I guess I agree that using R² does provide an easier way to understand what you mean however there is no sign on R².
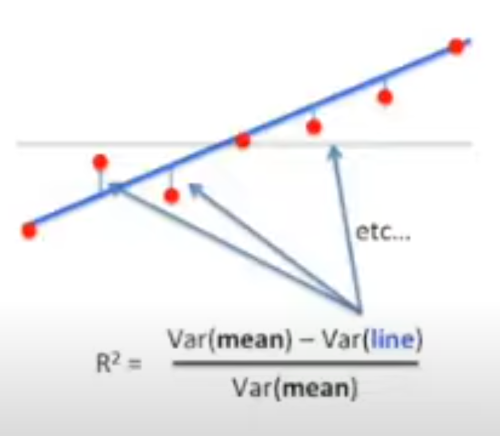
Formula for R²
This is given by
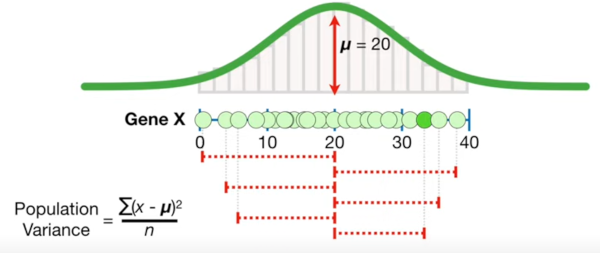
A reminder of how we calculate variance, we add up the differences from the mean like below. Note this shows a population and we should divide by n-1 not n but I liked the graphic.
This was a nice picture
