R Squared

Introduction

This is all about R².

My Thoughts

Least Squares Review

Most of this requires you to think about a dataset with lots of points. What we are trying to do is with least squares is find the best fit for a line for our data points. Once we have this we could maybe predict for a new data point what the y-value might be given the x-value. Here is the formula
$S=\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$
And here is an example of usage

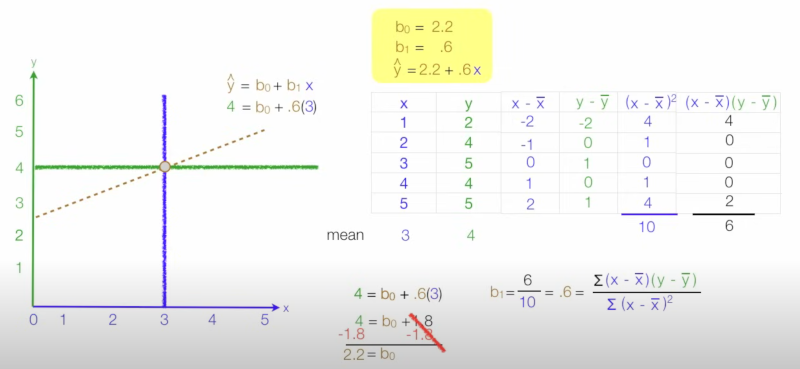
R Squared

With $R^2$ we are looking at the variances (changes) using the mean and the line. Squaring means we don't care about negative or positive.

What is the difference

Well I guess R² = R squared. R² is the variance between a dependent variable and an independent variable in terms of percentage. Therefore 0.4 R² = 40% and R = 0.2. I guess I agree that using R² does provide an easier way to understand what you mean however there is no sign on R².

Formula for R²

This is given by

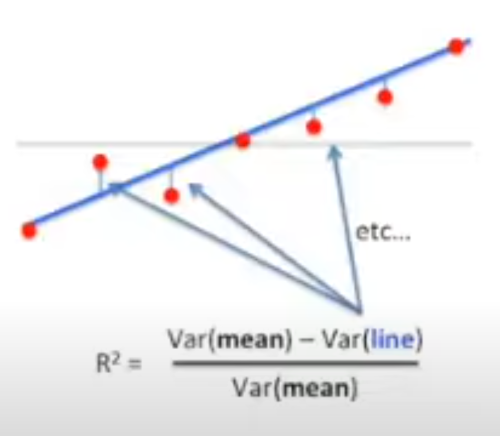
A reminder of how we calculate variance, we add up the differences from the mean like below. Note this shows a population and we should divide by n-1 not n but I liked the graphic.

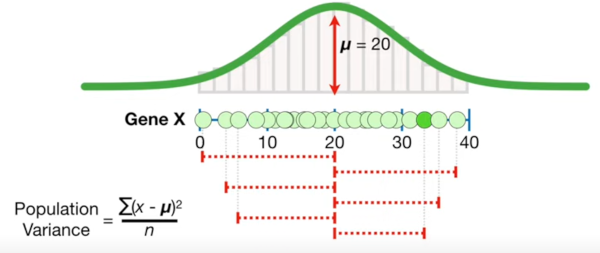
This was a nice picture

F

So we know this is formula for $R^2$
$R^2=\frac{{\text{SS}}_{\text{model}}}{{\text{SS}}_{\text{tot}}}$
Where

• ${\text{SS}}_{\text{res}}$ is the sum of squared residuals, which measures the variability of the observed data around the predicted values.
• ${\text{SS}}_{\text{tot}}$ is the total sum of squares, which measures the variability of the observed data around the mean.

So now we move on to F
$F=S{S}_{\text{mean}}-\frac{\frac{S{S}_{\text{fit}}}{Pfit-Pmean}}{\frac{S{S}_{\text{fit}}}{n-Pfit}}$

• 𝑆𝑆 mean: Represents the sum of squares around the mean.
• 𝑆𝑆 fit: Represents the sum of squares explained by the fit or model.
• 𝑃𝑓𝑖𝑡−𝑃𝑚𝑒𝑎𝑛: Captures the difference between individual predicted values (𝑃𝑓𝑖𝑡) and their mean (𝑃𝑚𝑒𝑎𝑛).
• 𝑛−𝑃𝑓𝑖𝑡: Adjusts for the total observations relative to predicted fit values.