Verilog

Introduction

Dipping my toe into this now I own an fpga

Boolean Algebra

Hardest thing about this is the amount of different symbols which mean the same thing.

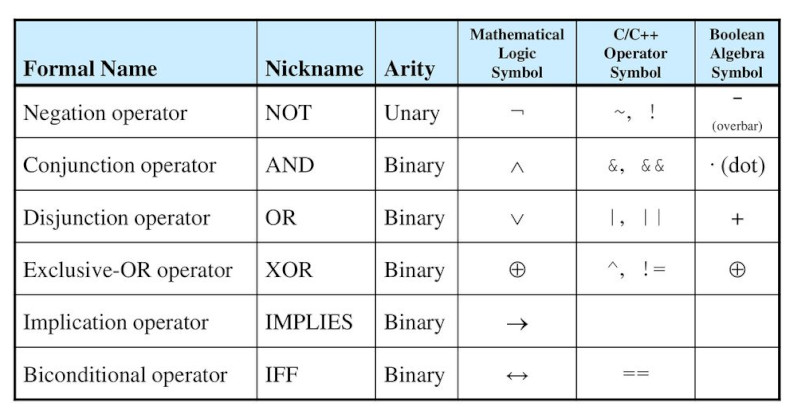
I guess each party wanted there own way. Here are the gates as seen on a circuit diagram

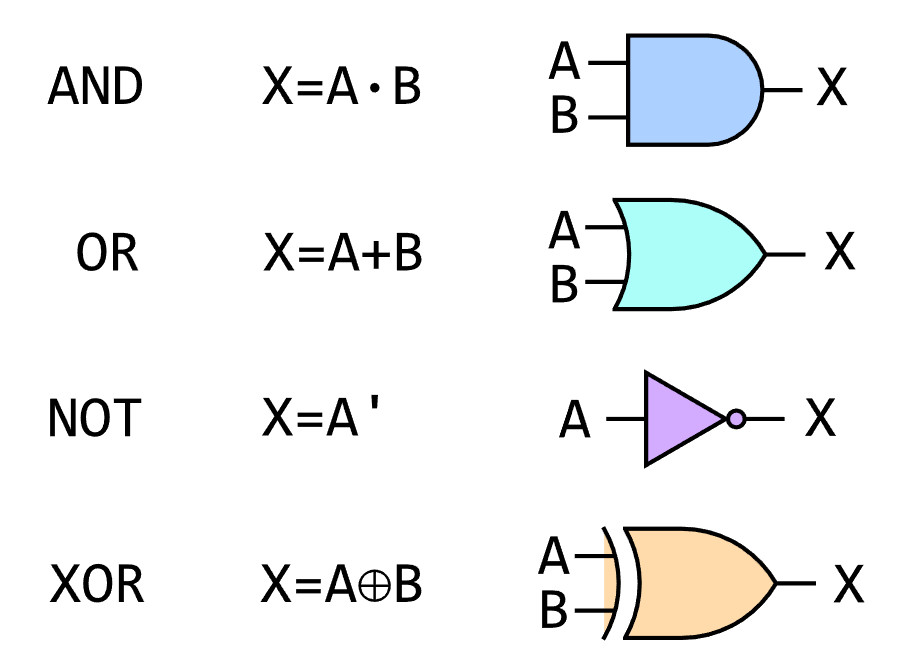
And of course someone else knew better. Here is IEEE version but given the amount of googling to get one nice enough I am guessing these are not popular

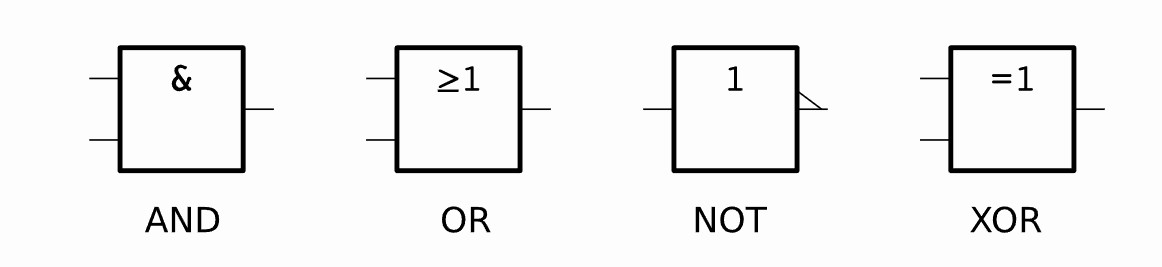
This seemed to be the popular way for documentr a truth table where NOT uses a macron over the value to indicate inverted (negated) value.

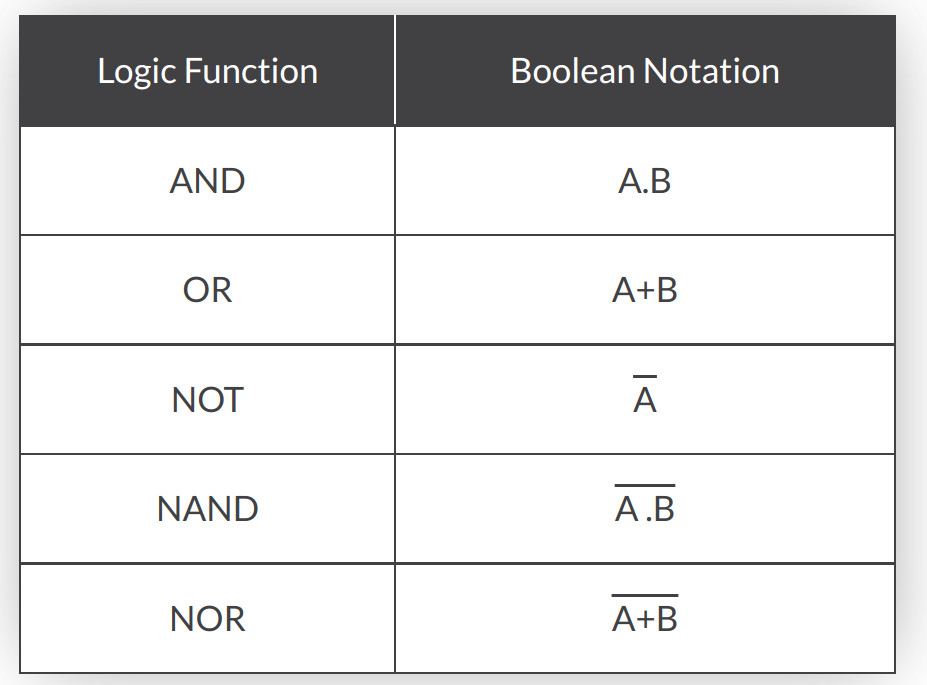
Boolean Laws

Commutative Law

Any binary operation which satisfies the following expression is referred to as a commutative operation. Commutative law states that changing the sequence of the variables does not have any effect on the output of a logic circuit.

• A. B = B. A
• A + B = B + A

Associative Law

It states that the order in which the logic operations are performed is irrelevant as their effect is the same.

• ( A. B ). C = A . ( B . C )
• ( A + B ) + C = A + ( B + C)

Distributive Law

Distributive law states the following conditions:

• A. ( B + C) = (A. B) + (A. C)
• A + (B. C) = (A + B) . ( A + C)

AND Law

These laws use the AND operation. Therefore they are called AND laws.

• A .0 = 0
• A . 1 = A
• A. A = A

OR Law

These laws use the OR operation. Therefore they are called OR laws.

• A + 0 = A
• A + 1 = 1
• A + A = A

Inversion Law

In Boolean algebra, the inversion law states that double inversion of variable results in the original variable itself.

Boolean Algebra Theorems

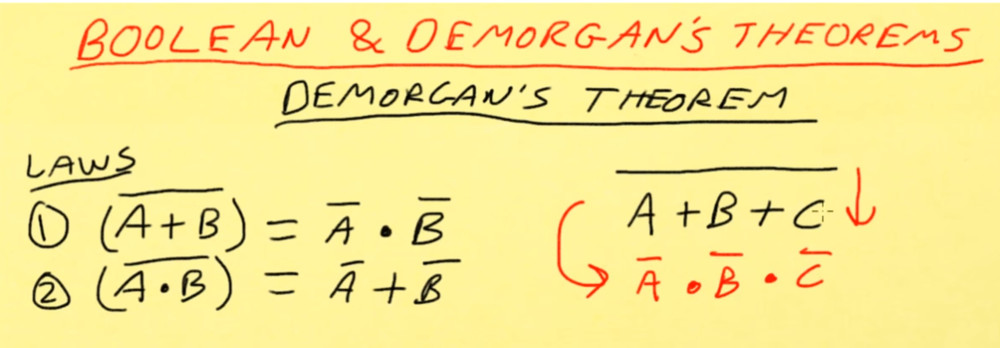
De Morgan’s First Law

De Morgan’s First Law states that the complement of the product of the variables is equal to the sum of their individual complements of a variable.

(A.B)’ = A’+B’

or

¬(A.B) = ¬A + ¬B

or

¬(A AND B) = ¬A OR ¬B

De Morgan’s Second Law

The second law states that the complement of the sum of variables is equal to the product of their individual complements of a variable.

(A+B)’ = A’.B’

or

¬(A+B) = ¬A . ¬B

or

¬(A OR B) = ¬A AND ¬B

Why Always me favourite Question

When we put logic on a circuit we can use these to help reduce the amount of components, therefore cost and errors.

A little distraction Universal Gates

During the demonstration of using the De Morgon theorems, it was shown that you can make any gate from either NAND or NOR gates so thought I might put these here.

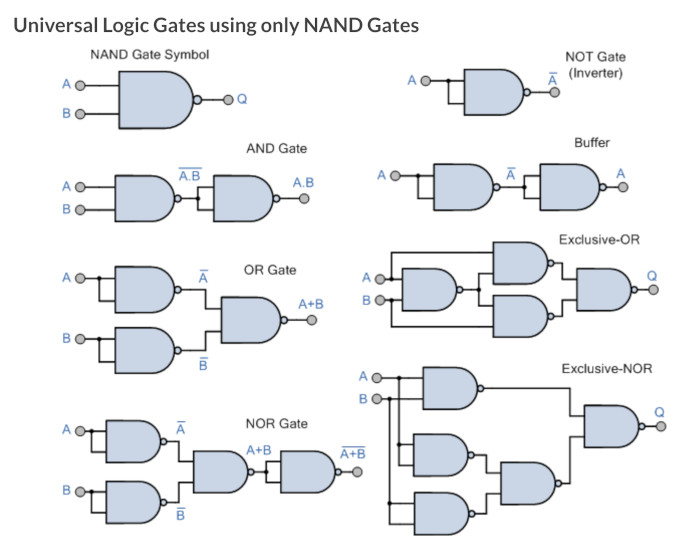
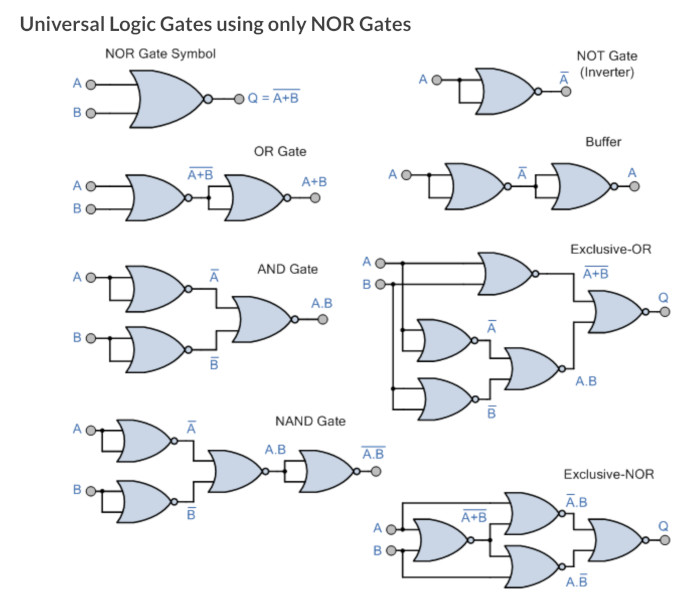
Back to Dave

Here is an example for Dave a eevblog (my hero today)

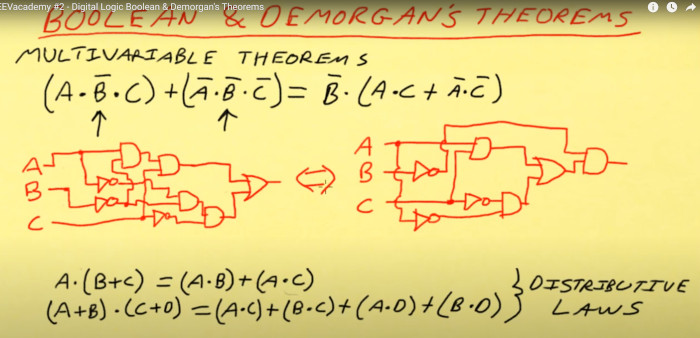
Using the above knowledge we have reduced the components from 5 input gates, 3 invertors, to 4 input gates, 3 invertors just using the distributive laws. Below is Dave explaining an easy way to remember De Morgans's first theroem. Drop the bar and change the sign

Hello World

This is the first program. There are two files to get it to work, a pcf file which defines things you use in the verilog file. Currently my understanding is it maps hardware to names which you can reference in the verilog file. Here is the project. I only use two buttons in the example but there are four shown for the second example
==Requirements For the requirements we have only light when both buttons are pressed.

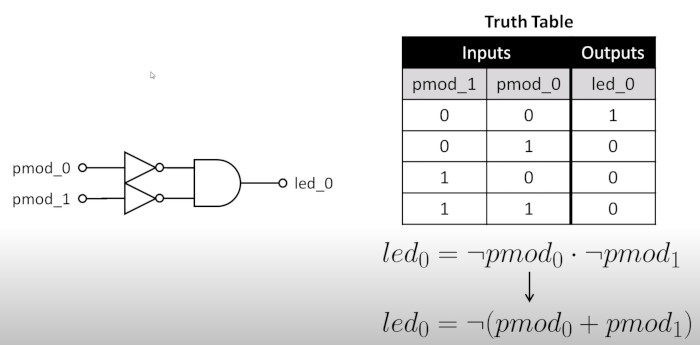
Truth Table

We can express this as a circuit diagram and a truth table. We need to understand some boolean algebra to understand the truth table

PCF Physical Constraints File (and_gate.pcf)

Could not find a lexer but here we define names to io pins. You lookup the pin in the datasheet, in my case a ice40UP5K-B-EVN and you assign a name.

#LED 
set_io              led_0  41

#HEADER B I/O
set_io  -pullup yes pmod_0 23
set_io  -pullup yes pmod_1 25

Verilog File (and_gate.v)

Here is my first program, it defines two input buttons and 1 LED in a module called and_gate. The value of LED is true when pmod_0 and pmod_1 are true.

module and_gate (
    // inputs
    input   pmod_0,
    input   pmod_1,

    // Outputs
    output  led_0
);

    assign led_0 = ~pmod_0 & ~pmod_1;
    
endmodule