Verilog

Introduction

Dipping my toe into this now I own an fpga

Hello World

This is the first program. There are two files to get it to work, a pcf file which defines things you use in the verilog file. Currently my understanding is it maps hardware to names which you can reference in the verilog file. Here is the project. I only use two buttons in the example but there are four shown for the second example
==Requirements For the requirements we have only light when both buttons are pressed.

Truth Table

We can express this as a circuit diagram and a truth table. We need to understand some boolean algebra to understand the truth table

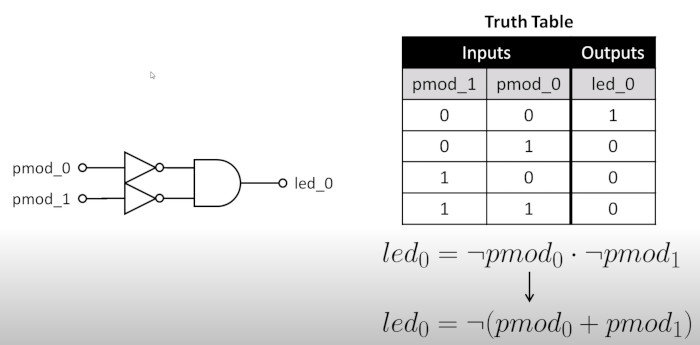
PCF Physical Constraints File (and_gate.pcf)

Could not find a lexer but here we define names to io pins. You lookup the pin in the datasheet, in my case a ice40UP5K-B-EVN and you assign a name.

#LED 
set_io              led_0  41

#HEADER B I/O
set_io  -pullup yes pmod_0 23
set_io  -pullup yes pmod_1 25

Verilog File (and_gate.v)

Here is my first program, it defines two input buttons and 1 LED in a module called and_gate. The value of LED is true when pmod_0 and pmod_1 are true.

module and_gate (
    // inputs
    input   pmod_0,
    input   pmod_1,

    // Outputs
    output  led_0
);

    assign led_0 = ~pmod_0 & ~pmod_1;
    
endmodule

Hello World 2

Well now we have the basics we can add some more verilog stuff. We can reference the inputs and outputs as arrays. We are now going to build a circuit where if we press 1 button, 2 LEDs light up and if we press 2 buttons 2 LED light up. This is shown in the circuit diagram and truth table below

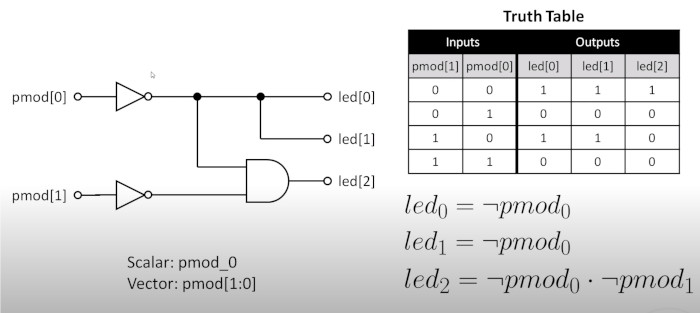
PCF Physical Constraints File (and_gate.pcf)

Not we can put the hardware in array to make the verilog file simpler

#LED 
set_io    led[0]  23
set_io    led[1]  25
set_io    led[2]  26
#set_io    led[3]  27
#set_io    led[4]  32

set_io  -pullup yes pmod[0] 36
set_io  -pullup yes pmod[1] 42

#set_io  -pullup yes pmod_2 12
#set_io  -pullup yes pmod_3 14

Verilog File (and_gate.v)

Here is my first program. We basically create a name for the wiring not_pod_0 and assign LED 0,1 to one value and LED 2 to another.

module and_gate (
    // inputs
    input   [1:0] pmod,

    // Outputs
    output  [2:0] led
);

    // Wire declaration
    wire not_pod_0;

    // Continuous Assignment replicate 1 wire to two outputs
    assign not_pmod_0 = ~pmod[0];
    assign led[1:0] = {2{not_pmod_0}};

    // Continuous Assignment: NOT and AND operators
    assign led[2] = not_pmod_0 & ~pmod[1];
    
endmodule

True Adder

Truth Table

Next we make a truth adder using the following
The Cᵢₙ represents the carry value. So you add A + B and the carry to get column S. If there is a carry then Cₒᵤₜ is 1

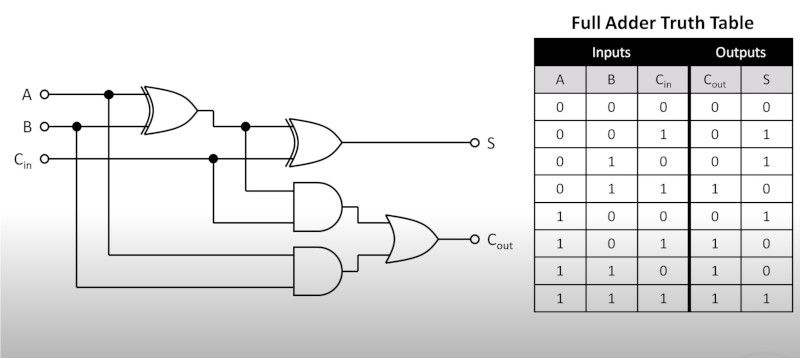
Boolean Algebra representation

Doing my own attempt and it took a couple because it is hard to see the bars and we have

S    = (A̅.B̅.C ) +  (A̅.B.C̅) + (A.B̅.C̅) + (A.B.C)
Cₒᵤₜ = (A̅.B.C ) +  (A.B̅.C) + (A.B.C̅) + (A.B.C̅)

Now we need to simplify

Simplification of S

Here is the Simplification of S

Lets take C as common and pair up with 1st and 4th expression and 2 and 3

=> C ( A̅.B̅ + A.B )  + C̅ (A̅.B + A.B̅)
   
Found this a bit tricky to wrote up the XOR and NOR above. Basically A̅.B̅ + A.B = A̅ ⊕ B̅ - XOR and A̅.B + A.B̅ = A ⊕ B - NOR
=> C ( A̅ ⊕ B̅ ) + C̅ ( A ⊕ B)
 
Lets substitute A̅ ⊕ B̅ = x this gives
=> Cx̅ + C̅x Compliments result in XOR
=> C ⊕ x 
 
 Substituting x back in
=> C ⊕ A ⊕ B

Simplification of Cₒᵤₜ

Here is the Simplification of Cₒᵤₜ

 Lets take C as common for 1 and 2 and AB to 3 and 4
=> C ( A̅B + AB̅) + AB (C + C̅)

 Using OR law (Z + Z̅ = 1) we can apply this to the Right hand side

=> C ( A̅B + AB̅) + AB

 Using compliments

=> C (A̅ ⊕ B̅) + AB

PCF File

Perhaps the only part I found simple

#LEDS 
set_io    led[0]  23
set_io    led[1]  25
set_io    led[2]  26
set_io    led[3]  27
set_io    led[4]  32

#Push Buttons
set_io  -pullup yes pmod[0] 36
set_io  -pullup yes pmod[1] 42
set_io  -pullup yes pmod[2] 38
set_io  -pullup yes pmod[3] 28

Verilog File

Not that hard but do need to understand there result. Here is mine

module full_adder (

    // Inputs
    input   [2:0]   pmod,
    
    // Output
    output  [1:0]   led
);
    wire A;
    wire B;
    wire C;

    // Set A, B, and C  to buttons and off
    assign A = ~pmod[0];
    assign B = ~pmod[1];
    assign C = ~pmod[2];

    // Taken from above working
    // led[0] C (A̅ ⊕ B̅) + AB
    // led[1] C ⊕ A ⊕ B

    // Cout
    assign led[0] = (C & (!A ^ !B) ) | (A & B);

    // S
    assign led[1] = C ^ A ^ B;

    
endmodule

Digi-Keys Solution

Learning Verilog using the digi-key [tutorial]. Mine works but as is my want I need to understand the differences

• leds are reversed
• led[0] and my solution are identical we just need to define a_xor_b
• led[1] I need to understand how ( (a ^ b) & c_in) in their solution = (C & (!A ^ !B) ) in my solution

So here is my explanation for why (A ^ B) = (!A ^ !B)

 We know A ^ B =  A!B + !AB because of the XOR above
 If we substitute A and B with there negatives
 We get A!B + !AB which is A^B

module full_adder (

    // Inputs
    input   [2:0]   pmod,
    
    // Output
    output  [1:0]   led
);

    // Wire (net) declarations (internal to module)
    wire a;
    wire b;
    wire c_in;
    wire a_xor_b;
    
    // A, B, and C_IN are inverted button logic
    assign a = ~pmod[0];
    assign b = ~pmod[1];
    assign c_in = ~pmod[2];
    
    // Create intermediate wire (net)
    assign a_xor_b = a ^ b;

    // Create output logic
    assign led[0] = a_xor_b ^ c_in;
    assign led[1] = (a_xor_b & c_in) | (a & b);
endmodule

Always and Registers

The next example is to demonstrate how these work. Hopefully comments in line make it obvious

module button_counter (

    // Inputs
    input   [2:0]   pmod,
    
    // Output
    output  reg [3:0]   led
);

    wire rst;
    wire clk;

    assign rst = ~pmod[0];
    assign clk = ~pmod[1];

    // Like a loop
    // while(clk or rst) {
    //   if(rst){
    //     led[0-3] = b0 
    //   } else {
    //     led[ led[current] +1] = b1
    //   }
    // }
     
    always @(posedge clk or posedge rst) begin
        if(rst == 1'b1) begin
            led <= 4'b0;
        end else begin
            led <= led + 1'b1;
        end
    end
endmodule

Clocks

Got this to work and understood it. Cannot seem to replace clock with crystal clearly more to learn.

module button_counter (

    // Inputs
    input               clk,
    input               rst_btn,   

    // Output
    output  reg [3:0]   led
);
    wire rst;

    // Create some registers
    reg div_clk;
    reg [31:0] count;

    // 10110111000110110000000 = 6000000 in Binary

    localparam [31:0] max_count = 6000000;
 
    // Reset is the inverse of the reset button
    assign rst = ~rst_btn;

    // Count up on (divided) clock rising edge or reset on button push
    // while (div_clk or reset) {
    //    if (reset == 1) {
    //       led[0-3] = 0
    //    }   
    //    else {
    //       led[ led[current] +1] = b1 
    //    }
    // }
    always @ (posedge div_clk or posedge rst) begin
        if (rst == 1'b1) begin
            led <= 4'b0;
        end else begin
            led <= led + 1'b1;
        end
    end

    // Count up on (divided) clock rising edge or reset on button push
    // while (clk or reset) {
    //    if (reset == 1) {
    //       count[0-31] = 0 
    //    }   
    //    else if (count = max_count) {
    //       count[0-31] = 0 
    //       div_clk = !div_clk;
    //    }
    //    else {
    //       count = count +1
    //    }
    // }
    always @ (posedge clk or posedge rst) begin
        if (rst == 1'b1) begin
            count <= 32'b0;
        end else if (count == max_count) begin
            count <= 32'b0;
            // Revisiting this, it was this line I struggled with but the answer is pretty easy
            // One invert the value if the max_count has been achieved. We invert because we don't know if it is one or zero
            div_clk <= ~div_clk;
        end else begin
            count <= count + 1;
        end
    end
    
endmodule

Mealy and Moore Finite State Machines (FSM)

Finite State Machines

Thought I knew about these. Turns out I need to match knowledge to theory. Here is how we show finite state machines. Either with a table or a diagram. The circles represent states and the double circles are what is called accepeting states.

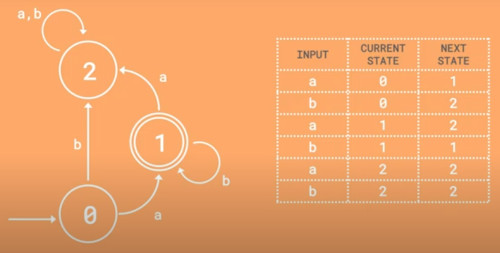
Working through the logic we find it is just fancy language which is good because we can communicate and understand each other.

• Q is a finite set of states.
• ∑ is a finite set of symbols called the alphabet.
• 8δ is the transition function where δ: Q × ∑ → Q
• q0 is the initial state from where any input is processed (q0 ∈ Q).
• F is a set of final state/states of Q (F ⊆ Q).

Looking at the video kinda explained it all. Note there is a arrow usually to show the start state.

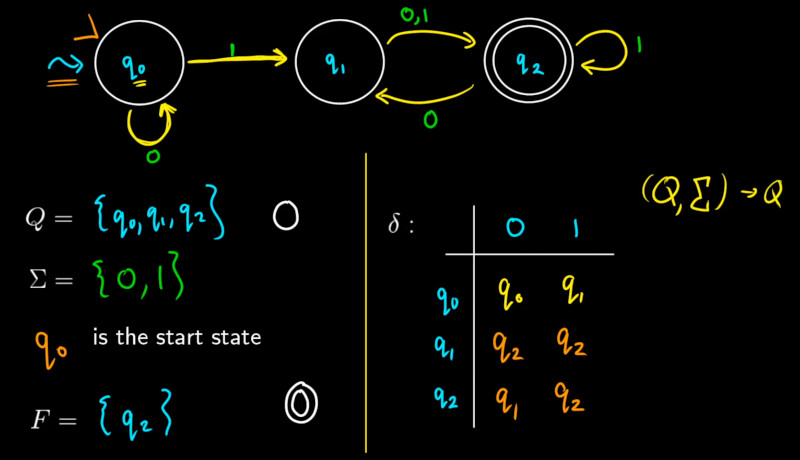
Verilog Example

Moore and Mearly State Machine

In the example we were shown both moore and mealy state machines for the same requirements
Moore

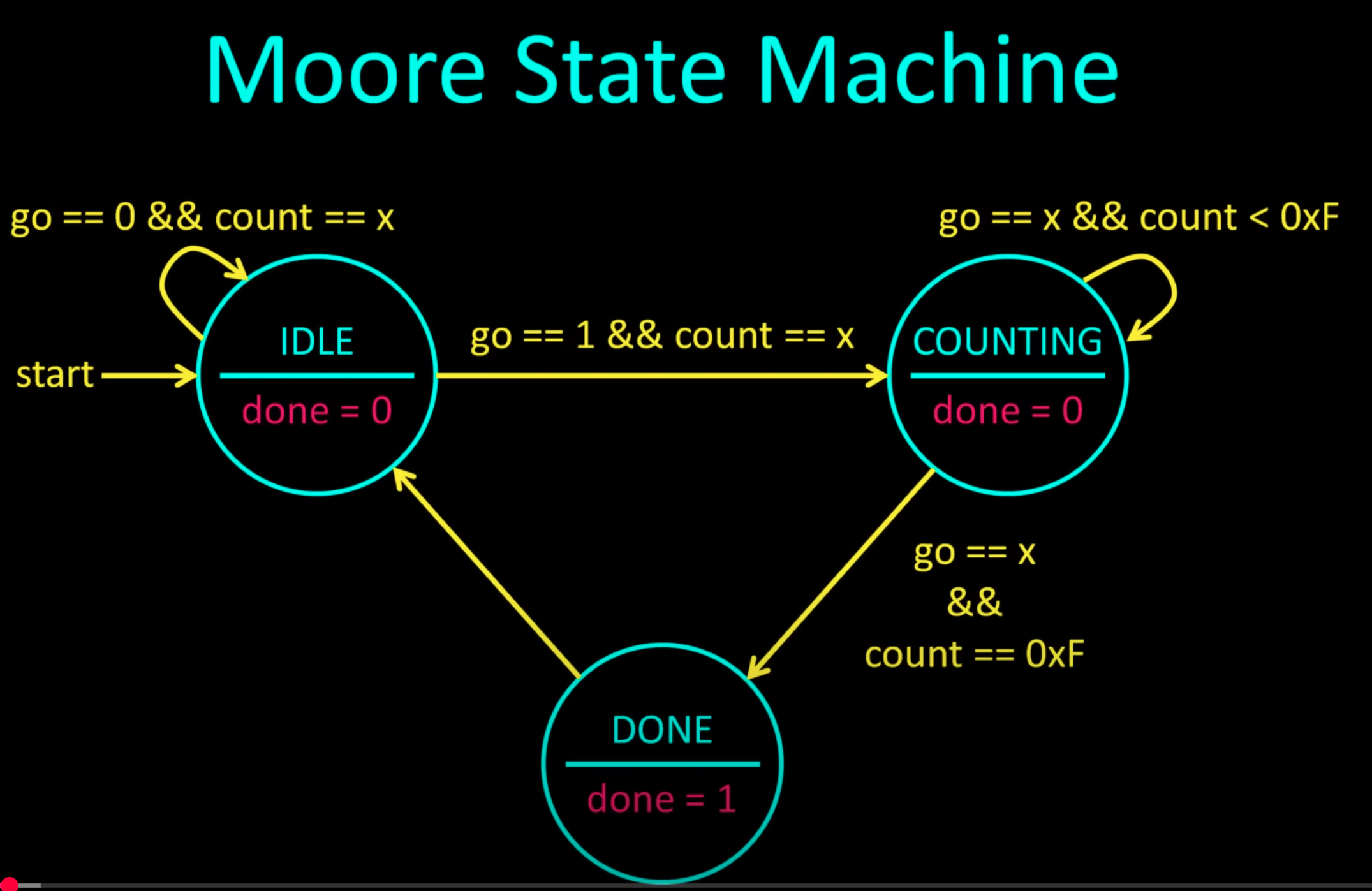
Mealy


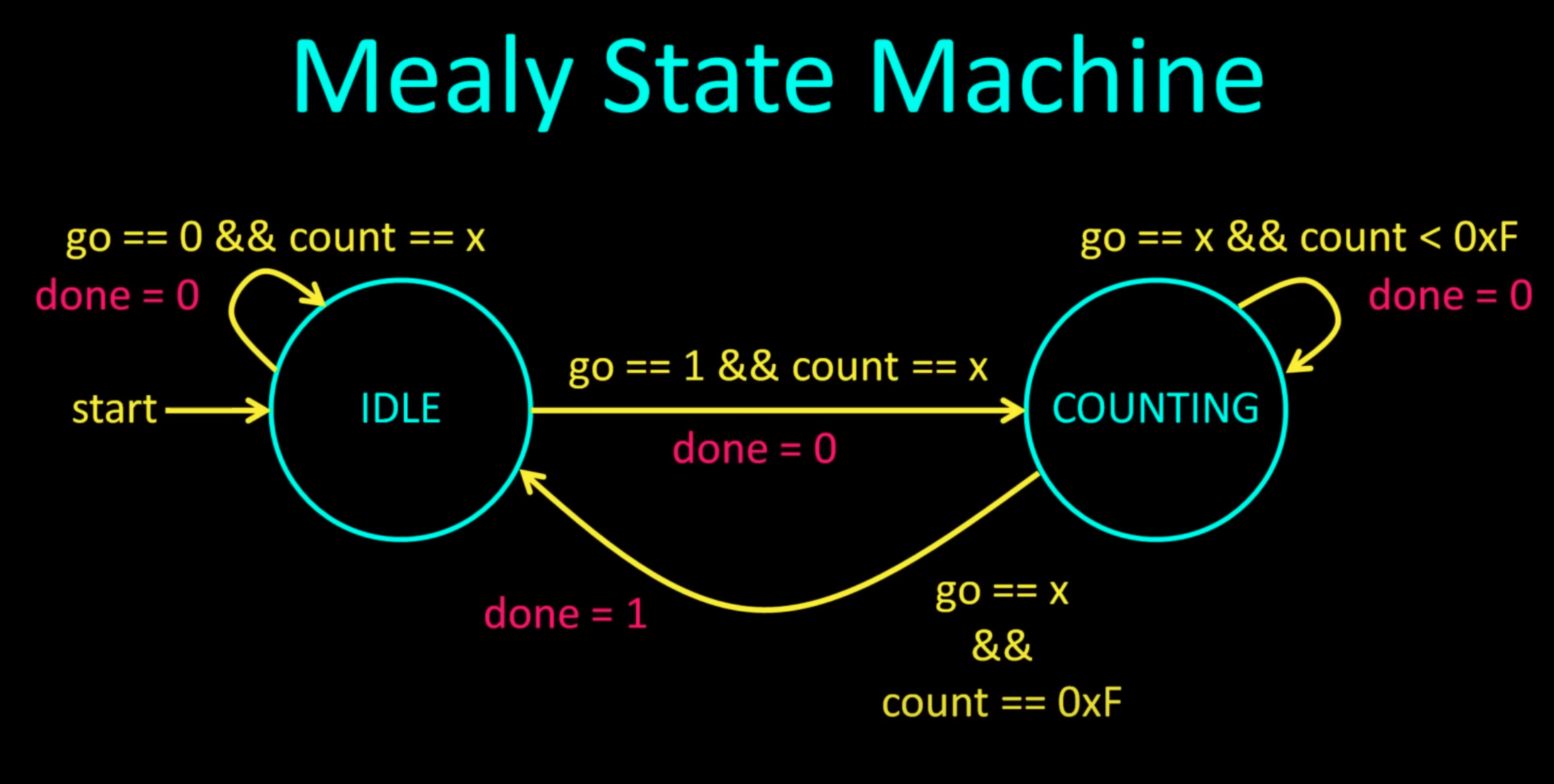
A chapter that actually made sense.

module mealy_fsm (

    // Inputs
    input               clk,
    input               rst_btn,
    input               go_btn,
    
    // Outputs
    output  reg [3:0]   led,
    output  reg         done_sig
);

    // States
    localparam STATE_IDLE       = 2'd0;
    localparam STATE_COUNTING   = 2'd1;    
    localparam STATE_DONE       = 2'd2;
    
    // Not the letter before the value is the type
    // b = binary
    // d = decimal
    // h = hex
    // Max counts for clock divider and counter
    localparam MAX_CLK_COUNT    = 24'd1500000;
    localparam MAX_LED_COUNT    = 4'hf;
    
    // Internal signals
    wire rst;
    wire go;
    
    // Internal storage elements
    reg         div_clk;
    reg [1:0]   state;
    reg [23:0]  clk_count;
    
    // Invert active-low buttons
    assign rst = ~rst_btn;
    assign go = ~go_btn;

    // clock divider no change except for values    
    always @ (posedge clk or posedge rst) begin
        if (rst == 1'b1) begin
            clk_count <= 24'b0;
        end else if (clk_count == MAX_CLK_COUNT) begin
            clk_count <= 24'b0;
            div_clk <= ~div_clk;
        end else begin
            clk_count <= clk_count + 1;
        end
    end


    // State transition logic
    always @ (posedge div_clk or posedge rst) begin
    
        // On reset, return to idle state and restart counters
        if (rst == 1'b1) begin
            state <= STATE_IDLE;
            
        // Define the state transitions
        end else begin
            case (state)
            
                // Wait for go button to be pressed
                STATE_IDLE: begin
                    if (go == 1'b1) begin
                        state <= STATE_COUNTING;
                    end
                end
            
                // Go from counting to done if counting reaches max
                STATE_COUNTING: begin
                    if (led == MAX_LED_COUNT) begin
                        state <= STATE_DONE;
                    end
                end
                    
                // Default case: return to idle state
                default: state <= STATE_IDLE;
            endcase
        end
    end
    
    // Run counter if in wait state
    always @ (posedge div_clk or posedge rst) begin
        if (rst == 1'b1) begin
            led <= 4'd0;
        end else begin
            if (state == STATE_COUNTING) begin
                led <= led + 1;
            end else begin
                led <= 4'd0;
            end
        end
    end
    
    always @ ( * ) begin
        if (state == STATE_DONE) begin
            done_sig = 1'b1;
        end else begin
            done_sig = 1'b0;
        end
    end

endmodule