Verilog

Introduction

Dipping my toe into this now I own an fpga

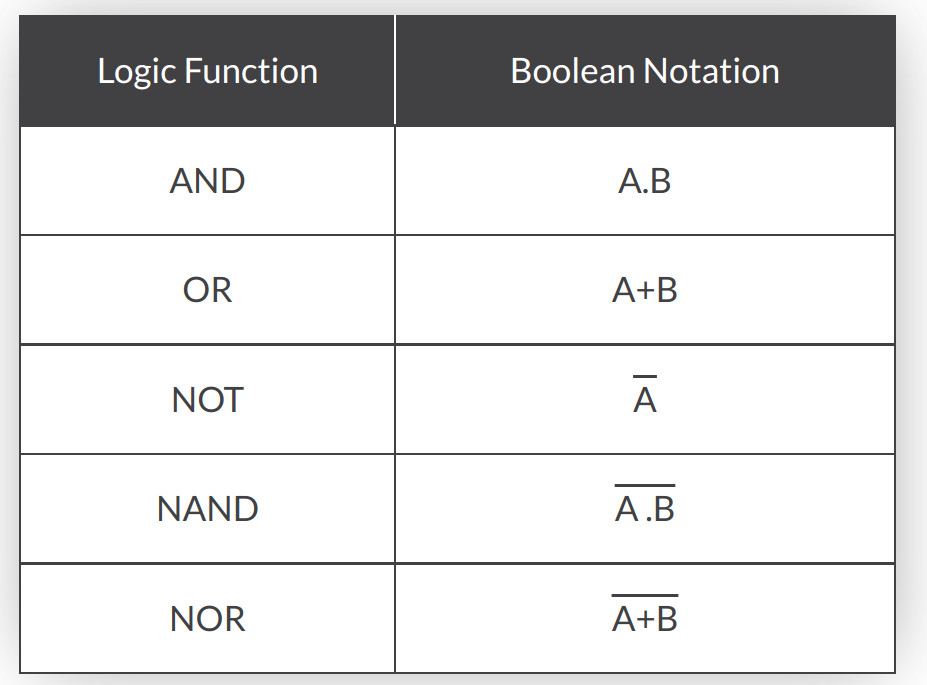
Boolean Algebra

Symbols (crash)

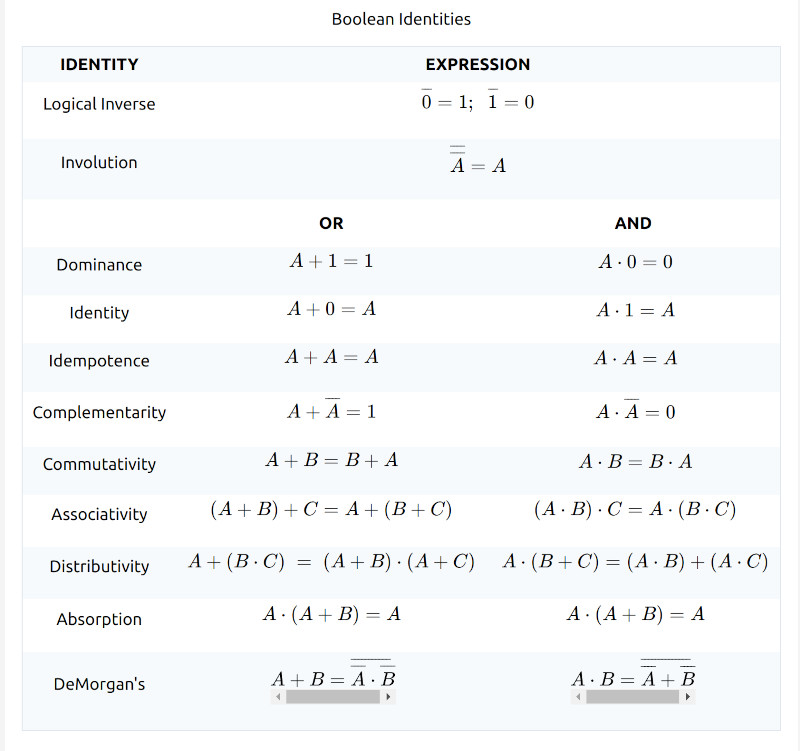
Hardest thing about this is the amount of different symbols which mean the same thing.

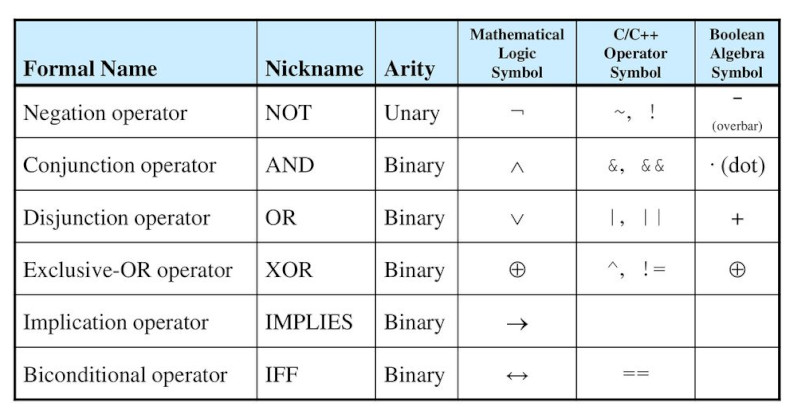
I guess each party wanted there own way. Here are the gates as seen on a circuit diagram

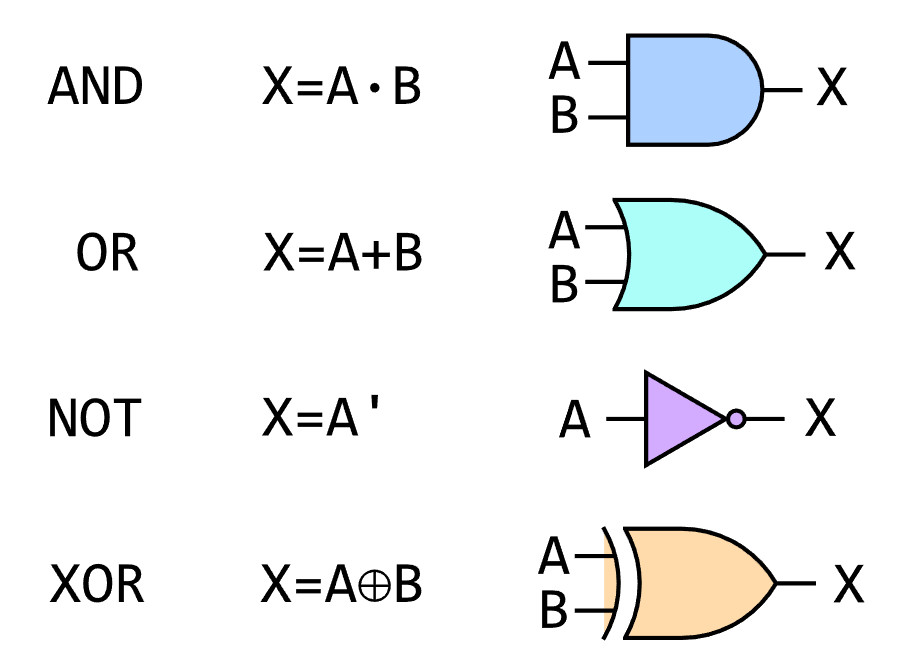
And of course someone else knew better. Here is IEEE version but given the amount of googling to get one nice enough I am guessing these are not popular

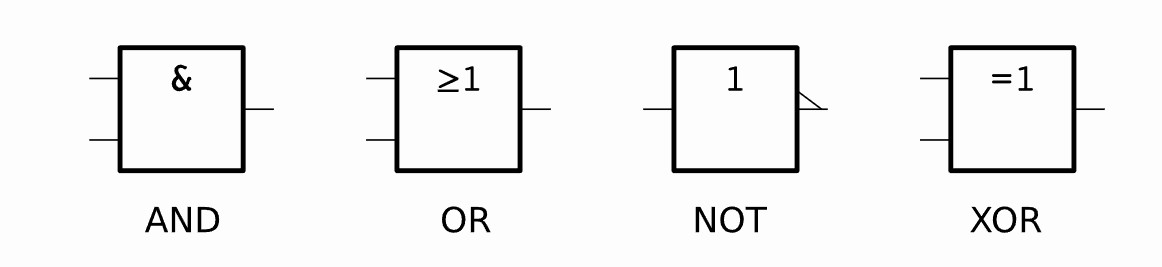
This seemed to be the popular way for documentr a truth table where NOT uses a macron over the value to indicate inverted (negated) value.

Order of Presidence

In regular maths we have PEMDAS for order of presidence apparantely which means

• P Parentheses first
• E Exponents (ie Powers and Square Roots, etc.)
• MD Multiplication and Division (left-to-right)
• AS Addition and Subtraction (left-to-right)

For Boolean Algebra we just have

• P Parentheses first e.g. ()
• I Inverses e.g. C̅.C̅
• P Products (.)
• S Sums (+)

Truth Tables and Gates

Here are all of the gates. We can see boolean expression and equivalents in the diagrams along with the truth tables.

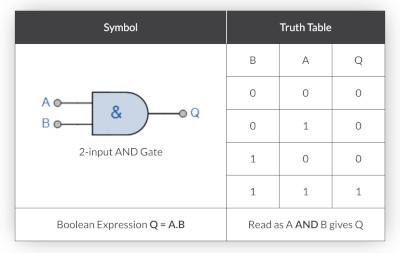
AND Gate

Here is the AND gate and truth table.

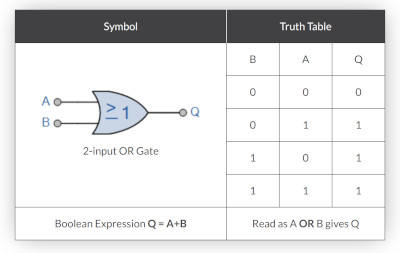
OR Gate

Here is the OR Gate and Truth table

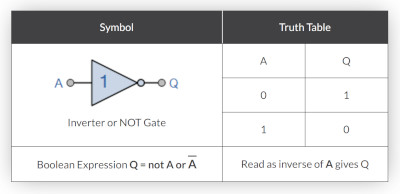
NOT Gate

Here is the NOT Gate and Truth table

NAND Gate

Here is the NAND Gate and Truth Table

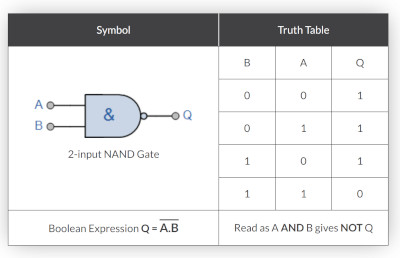
NOR Gate

And here is the NOR gate equivalent. It really is not as hard as it looks once you are in the zone. Right the truth table and the algebra and ezzy pezzy.

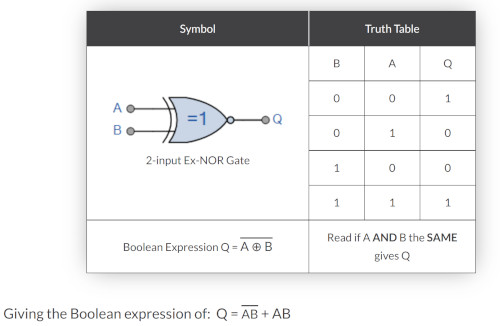
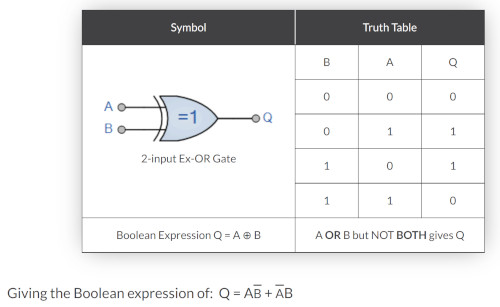
XOR Gate

I write this not in order. But further down I struggled with the boolean algebra for XOR gates and the substitution. Below is the explanation for which it works. Here is the truth table

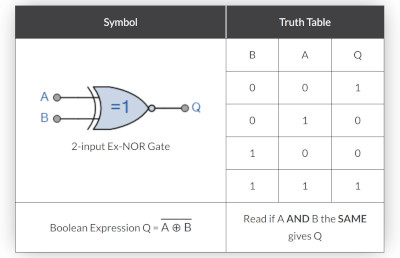
Exclusive XNOR Gate

Here is the Exclusive NOR Gate and truth table

Universal Gates

During the demonstration of using the De Morgon theorems, it was shown that you can make any gate from either NAND or NOR gates so thought I might put these here.

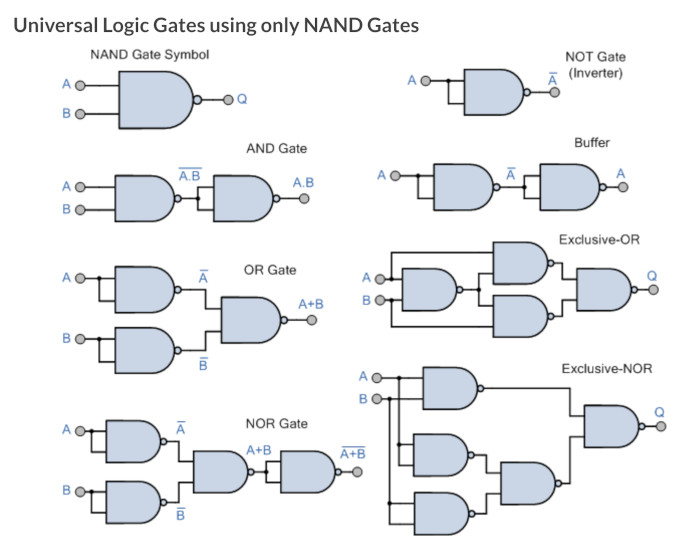
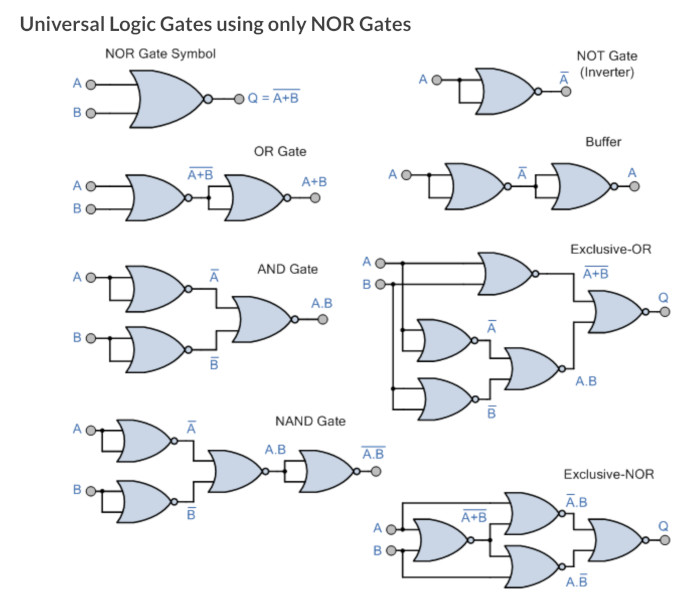
Proving Gates

In the youtube by Intermation they prove one of the expression equals another. And also shows

• Expression to prove
• Truth Table for expression and how to build it
• Physical Representation

He summarises that rationalisation reduces the power, increases the speed and reduces the cost and space.

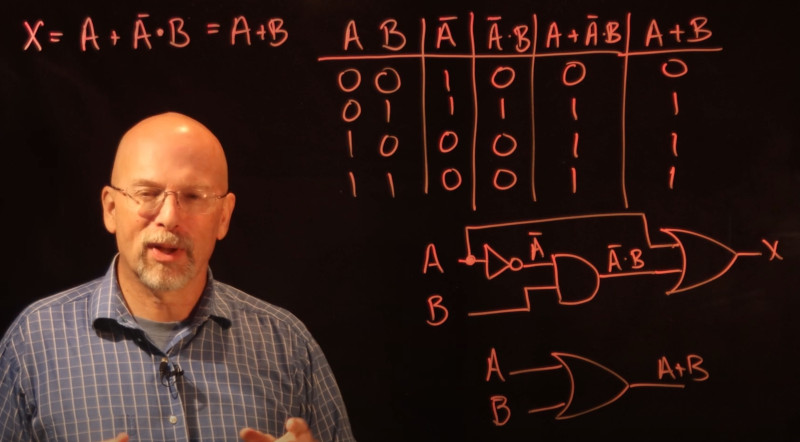
Identities Of Boolean

A new new phrase for me to google but this is about how to calculate result when a value is ANDed or ORed with itself for example. Not Shown in the slide but here is the XOR examples A⊕A examples

• A ⊕ A = 0
• A ⊕ A̅ = 1
• A ⊕ 1 = 1
• A ⊕ 1 = A̅
• A ⊕ 0 = 1

Boolean Laws

Commutative Law

Any binary operation which satisfies the following expression is referred to as a commutative operation. Commutative law states that changing the sequence of the variables does not have any effect on the output of a logic circuit.

• A. B = B. A
• A + B = B + A

Associative Law

It states that the order in which the logic operations are performed is irrelevant as their effect is the same.

• ( A. B ). C = A . ( B . C )
• ( A + B ) + C = A + ( B + C)

Distributive Law

Distributive law states the following conditions:

• A. ( B + C) = (A. B) + (A. C)
• A + (B. C) = (A + B) . ( A + C)

AND Law

These laws use the AND operation. Therefore they are called AND laws.

• A .0 = 0
• A . 1 = A
• A. A = A

OR Law

These laws use the OR operation. Therefore they are called OR laws.

• A + 0 = A
• A + 1 = 1
• A + A = A

Inversion Law

In Boolean algebra, the inversion law states that double inversion of variable results in the original variable itself.

Boolean Algebra Theorems

De Morgan’s First Law

De Morgan’s First Law states that the complement of the product of the variables is equal to the sum of their individual complements of a variable.

(A.B)’ = A’+B’

or

¬(A.B) = ¬A + ¬B

or

¬(A AND B) = ¬A OR ¬B

De Morgan’s Second Law

The second law states that the complement of the sum of variables is equal to the product of their individual complements of a variable.

(A+B)’ = A’.B’

or

¬(A+B) = ¬A . ¬B

or

¬(A OR B) = ¬A AND ¬B

Worked XOR example

Really liked this explanation for XOR from youtube which combines all elements learning today. Truth tables are 2 to the power of inputs.

Why Always my favourite Question

When we put logic on a circuit we can use these to help reduce the amount of components, therefore cost and errors.

To Dave

Here is an example for Dave a eevblog (my hero today)


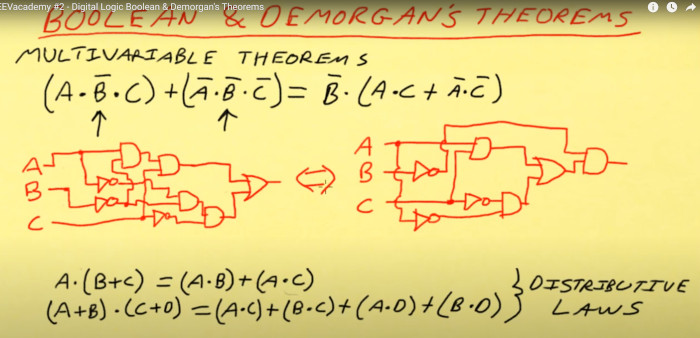
Using the above knowledge we have reduced the components from 5 input gates, 3 invertors, to 4 input gates, 3 invertors just using the distributive laws.

Below is Dave explaining an easy way to remember De Morgans's first theroem. Drop the bar and change the sign


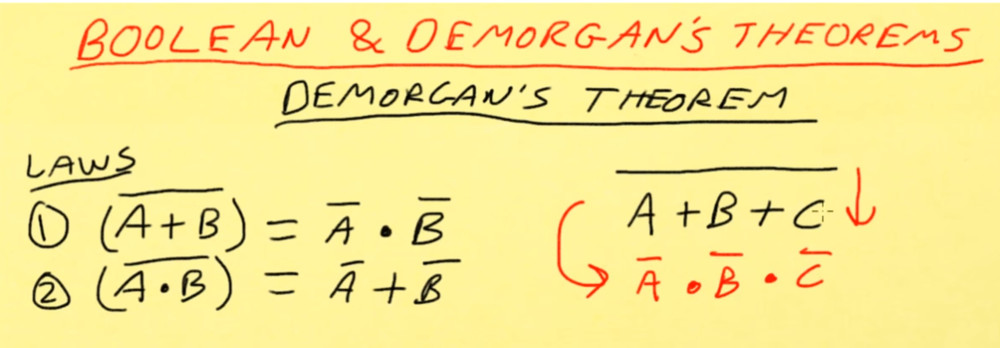
We can now start spotting patterns where we know we can reduce the gate count. Here we have two input NOR gates as inputs to a NOR gate. Using boolean algebra we can reduce this to an AND gate

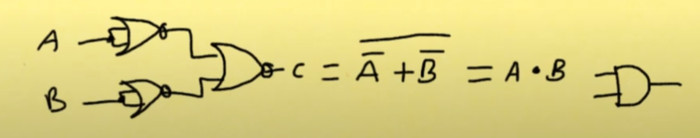
Hello World

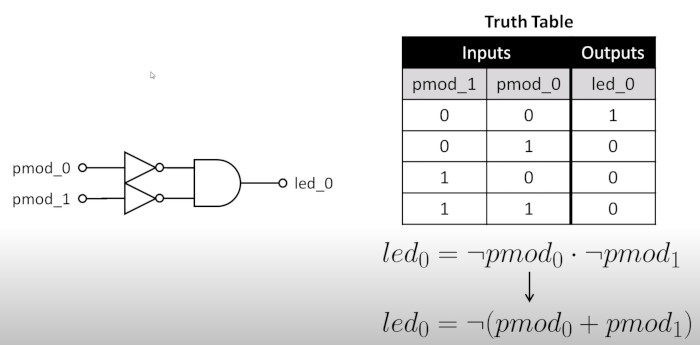
This is the first program. There are two files to get it to work, a pcf file which defines things you use in the verilog file. Currently my understanding is it maps hardware to names which you can reference in the verilog file. Here is the project. I only use two buttons in the example but there are four shown for the second example
==Requirements For the requirements we have only light when both buttons are pressed.

Truth Table

We can express this as a circuit diagram and a truth table. We need to understand some boolean algebra to understand the truth table

PCF Physical Constraints File (and_gate.pcf)

Could not find a lexer but here we define names to io pins. You lookup the pin in the datasheet, in my case a ice40UP5K-B-EVN and you assign a name.

#LED 
set_io              led_0  41

#HEADER B I/O
set_io  -pullup yes pmod_0 23
set_io  -pullup yes pmod_1 25

Verilog File (and_gate.v)

Here is my first program, it defines two input buttons and 1 LED in a module called and_gate. The value of LED is true when pmod_0 and pmod_1 are true.

module and_gate (
    // inputs
    input   pmod_0,
    input   pmod_1,

    // Outputs
    output  led_0
);

    assign led_0 = ~pmod_0 & ~pmod_1;
    
endmodule

Hello World 2

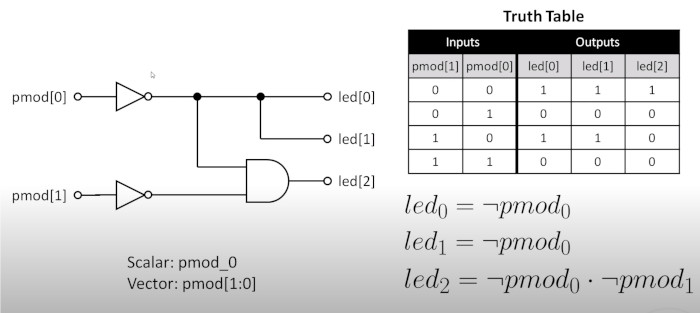
Well now we have the basics we can add some more verilog stuff. We can reference the inputs and outputs as arrays. We are now going to build a circuit where if we press 1 button, 2 LEDs light up and if we press 2 buttons 2 LED light up. This is shown in the circuit diagram and truth table below

PCF Physical Constraints File (and_gate.pcf)

Not we can put the hardware in array to make the verilog file simpler

#LED 
set_io    led[0]  23
set_io    led[1]  25
set_io    led[2]  26
#set_io    led[3]  27
#set_io    led[4]  32

set_io  -pullup yes pmod[0] 36
set_io  -pullup yes pmod[1] 42

#set_io  -pullup yes pmod_2 12
#set_io  -pullup yes pmod_3 14

Verilog File (and_gate.v)

Here is my first program. We basically create a name for the wiring not_pod_0 and assign LED 0,1 to one value and LED 2 to another.

module and_gate (
    // inputs
    input   [1:0] pmod,

    // Outputs
    output  [2:0] led
);

    // Wire declaration
    wire not_pod_0;

    // Continuous Assignment replicate 1 wire to two outputs
    assign not_pmod_0 = ~pmod[0];
    assign led[1:0] = {2{not_pmod_0}};

    // Continuous Assignment: NOT and AND operators
    assign led[2] = not_pmod_0 & ~pmod[1];
    
endmodule

True Adder

Truth Table

Next we make a truth adder using the following
The Cᵢₙ represents the carry value. So you add A + B and the carry to get column S. If there is a carry then Cₒᵤₜ is 1

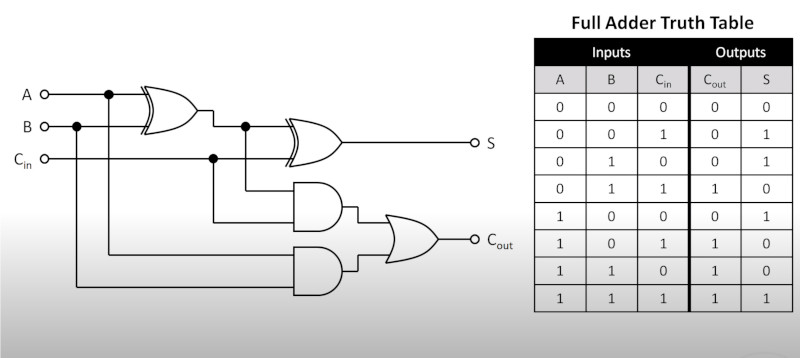
Boolean Algebra representation

Doing my own attempt and it took a couple because it is hard to see the bars and we have

S    = (A̅.B̅.C ) +  (A̅.B.C̅) + (A.B̅.C̅) + (A.B.C)
Cₒᵤₜ = (A̅.B.C ) +  (A.B̅.C) + (A.B.C̅) + (A.B.C̅)

Now we need to simplify

Simplification of S

Here is the Simplification of S

Lets take C as common and pair up with 1st and 4th expression and 2 and 3

=> C ( A̅.B̅ + A.B )  + C̅ (A̅.B + A.B̅)
   
Found this a bit tricky to wrote up the XOR and NOR above. Basically A̅.B̅ + A.B = A̅ ⊕ B̅ - XOR and A̅.B + A.B̅ = A ⊕ B - NOR
=> C ( A̅ ⊕ B̅ ) + C̅ ( A ⊕ B)
 
Lets substitute A̅ ⊕ B̅ = x this gives
=> Cx̅ + C̅x Compliments result in XOR
=> C ⊕ x 
 
 Substituting x back in
=> C ⊕ A ⊕ B

Simplification of Cₒᵤₜ

Here is the Simplification of Cₒᵤₜ

 Lets take C as common for 1 and 2 and AB to 3 and 4
=> C ( A̅B + AB̅) + AB (C + C̅)

 Using OR law (Z + Z̅ = 1) we can apply this to the Right hand side

=> C ( A̅B + AB̅) + AB

 Using compliments

=> C (A̅ ⊕ B̅) + AB

PCF File

Perhaps the only part I found simple

#LEDS 
set_io    led[0]  23
set_io    led[1]  25
set_io    led[2]  26
set_io    led[3]  27
set_io    led[4]  32

#Push Buttons
set_io  -pullup yes pmod[0] 36
set_io  -pullup yes pmod[1] 42
set_io  -pullup yes pmod[2] 38
set_io  -pullup yes pmod[3] 28

Verilog File

Not that hard but do need to understand there result. Here is mine

module full_adder (

    // Inputs
    input   [2:0]   pmod,
    
    // Output
    output  [1:0]   led
);
    wire A;
    wire B;
    wire C;

    // Set A, B, and C  to buttons and off
    assign A = ~pmod[0];
    assign B = ~pmod[1];
    assign C = ~pmod[2];

    // Taken from above working
    // led[0] C (A̅ ⊕ B̅) + AB
    // led[1] C ⊕ A ⊕ B

    // Cout
    assign led[0] = (C & (!A ^ !B) ) | (A & B);

    // S
    assign led[1] = C ^ A ^ B;

    
endmodule

Digi-Keys Solution

Learning Verilog using the digi-key [tutorial]. Mine works but as is my want I need to understand the differences

• leds are reversed
• led[0] and my solution are identical we just need to define a_xor_b
• led[1] I need to understand how ( (a ^ b) & c_in) in their solution = (C & (!A ^ !B) ) in my solution

So here is my explanation for why (A ^ B) = (!A ^ !B)

 We know A ^ B =  A!B + !AB because of the XOR above
 If we substitute A and B with there negatives
 We get A!B + !AB which is A^B

module full_adder (

    // Inputs
    input   [2:0]   pmod,
    
    // Output
    output  [1:0]   led
);

    // Wire (net) declarations (internal to module)
    wire a;
    wire b;
    wire c_in;
    wire a_xor_b;
    
    // A, B, and C_IN are inverted button logic
    assign a = ~pmod[0];
    assign b = ~pmod[1];
    assign c_in = ~pmod[2];
    
    // Create intermediate wire (net)
    assign a_xor_b = a ^ b;

    // Create output logic
    assign led[0] = a_xor_b ^ c_in;
    assign led[1] = (a_xor_b & c_in) | (a & b);
endmodule

Always and Registers

The next example is to demonstrate how these work. Hopefully comments in line make it obvious

module button_counter (

    // Inputs
    input   [2:0]   pmod,
    
    // Output
    output  reg [3:0]   led
);

    wire rst;
    wire clk;

    assign rst = ~pmod[0];
    assign clk = ~pmod[1];

    // Like a loop
    // while(clk or rst) {
    //   if(rst){
    //     led[0-3] = b0 
    //   } else {
    //     led[ led[current] +1] = b1
    //   }
    // }
     
    always @(posedge clk or posedge rst) begin
        if(rst == 1'b1) begin
            led <= 4'b0;
        end else begin
            led <= led + 1'b1;
        end
    end
endmodule

Clocks

Got this to work and understood it. Cannot seem to replace clock with crystal clearly more to learn.

module button_counter (

    // Inputs
    input               clk,
    input               rst_btn,   

    // Output
    output  reg [3:0]   led
);
    wire rst;

    // Create some registers
    reg div_clk;
    reg [31:0] count;

    // 10110111000110110000000 = 6000000
       0123456789 01234567890 12
    localparam [31:0] max_count = 6000000;
 
    // Reset is the inverse of the reset button
    assign rst = ~rst_btn;

    // Count up on (divided) clock rising edge or reset on button push
    // while (div_clk or reset) {
    //    if (reset == 1) {
    //       led[0-3] = 0
    //    }   
    //    else {
    //       led[ led[current] +1] = b1 
    //    }
    // }
    always @ (posedge div_clk or posedge rst) begin
        if (rst == 1'b1) begin
            led <= 4'b0;
        end else begin
            led <= led + 1'b1;
        end
    end

    // Count up on (divided) clock rising edge or reset on button push
    // while (clk or reset) {
    //    if (reset == 1) {
    //       count[0-31] = 0 
    //    }   
    //    else if (count = max_count) {
    //       count[0-31] = 0 
    //       div_clk = !div_clk;
    //    }
    //    else {
    //       count = count +1
    //    }
    // }
    always @ (posedge clk or posedge rst) begin
        if (rst == 1'b1) begin
            count <= 32'b0;
        end else if (count == max_count) begin
            count <= 32'b0;
            div_clk <= ~div_clk;
        end else begin
            count <= count + 1;
        end
    end
    
endmodule

Mealy and Moore Finite State Machines (FSM)

Finite State Machines

Thought I knew about these. Turns out I need to match knowledge to theory. Here is how we show finite state machines. Either with a table or a diagram. The circles represent states and the double circles are what is called accepeting states.

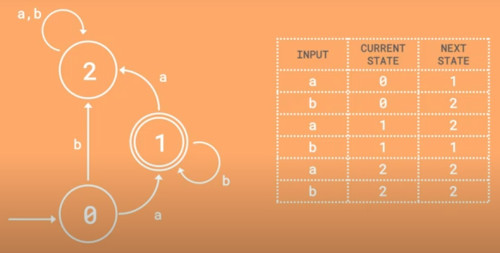
Working through the logic we find it is just fancy language which is good because we can communicate and understand each other.

• Q is a finite set of states.
• ∑ is a finite set of symbols called the alphabet.
• 8δ is the transition function where δ: Q × ∑ → Q
• q0 is the initial state from where any input is processed (q0 ∈ Q).
• F is a set of final state/states of Q (F ⊆ Q).

Looking at the video kinda explained it all. Note there is a arrow usually to show the start state.

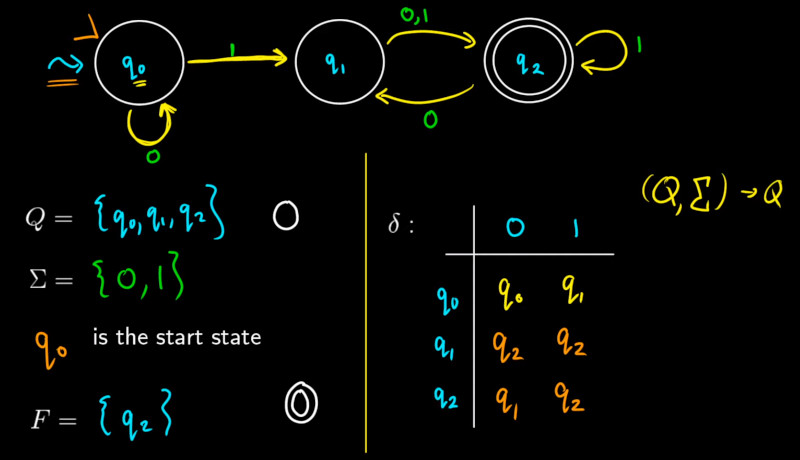
Verilog Example

A chapter that actually made sense.

module mealy_fsm (

    // Inputs
    input               clk,
    input               rst_btn,
    input               go_btn,
    
    // Outputs
    output  reg [3:0]   led,
    output  reg         done_sig
);

    // States
    localparam STATE_IDLE       = 2'd0;
    localparam STATE_COUNTING   = 2'd1;    
    localparam STATE_DONE       = 2'd2;
    
    // Not the letter before the value is the type
    // b = binary
    // d = decimal
    // h = hex
    // Max counts for clock divider and counter
    localparam MAX_CLK_COUNT    = 24'd1500000;
    localparam MAX_LED_COUNT    = 4'hf;
    
    // Internal signals
    wire rst;
    wire go;
    
    // Internal storage elements
    reg         div_clk;
    reg [1:0]   state;
    reg [23:0]  clk_count;
    
    // Invert active-low buttons
    assign rst = ~rst_btn;
    assign go = ~go_btn;

    // clock divider no change except for values    
    always @ (posedge clk or posedge rst) begin
        if (rst == 1'b1) begin
            clk_count <= 24'b0;
        end else if (clk_count == MAX_CLK_COUNT) begin
            clk_count <= 24'b0;
            div_clk <= ~div_clk;
        end else begin
            clk_count <= clk_count + 1;
        end
    end


    // State transition logic
    always @ (posedge div_clk or posedge rst) begin
    
        // On reset, return to idle state and restart counters
        if (rst == 1'b1) begin
            state <= STATE_IDLE;
            
        // Define the state transitions
        end else begin
            case (state)
            
                // Wait for go button to be pressed
                STATE_IDLE: begin
                    if (go == 1'b1) begin
                        state <= STATE_COUNTING;
                    end
                end
            
                // Go from counting to done if counting reaches max
                STATE_COUNTING: begin
                    if (led == MAX_LED_COUNT) begin
                        state <= STATE_DONE;
                    end
                end
                    
                // Default case: return to idle state
                default: state <= STATE_IDLE;
            endcase
        end
    end
    
    // Run counter if in wait state
    always @ (posedge div_clk or posedge rst) begin
        if (rst == 1'b1) begin
            led <= 4'd0;
        end else begin
            if (state == STATE_COUNTING) begin
                led <= led + 1;
            end else begin
                led <= 4'd0;
            end
        end
    end
    
    always @ ( * ) begin
        if (state == STATE_DONE) begin
            done_sig = 1'b1;
        end else begin
            done_sig = 1'b0;
        end
    end

endmodule