Sorting in Code
Jump to navigation
Jump to search
Selection Sort
Selection sort is when we iterate each position and try and get our smallest value each time. E.g. in python
def selection_sort(array):
m = len(array)
for i in range(m - 1):
# Assume the current index (i) has the minimum value
min_index = i
# Find the minimum element in the remaining unsorted part
for j in range(i + 1, m):
if array[j] < array[min_index]:
min_index = j
# Swap the found minimum element with the first element of the unsorted part
array[i], array[min_index] = array[min_index], array[i]
Looking at the code there are two for loops meaning this is O(n²)
And here it is in rust
fn selection_sort(numbers: &mut Vec<i32>) {
for i in 0..numbers.len() {
let mut min_index = i;
for j in i..numbers.len() {
if numbers[j] < numbers[min_index] {
min_index = j;
}
}
numbers.swap(i, min_index);
}
}
Bubble Sort
This was the first sort I did 40 years ago. Here in rust. Again this is this is O(n²)
fn bubble_sort(numbers: &mut Vec<i32>) {
for i in 0..numbers.len() {
for j in 0..numbers.len() - 1 {
if numbers[j] > numbers[j + 1] {
numbers.swap(j, j + 1);
}
}
}
}
There were improvements made in the course to the original answer where they identified code repeated even thought we knew the data was already sorted. A clear reason not to just cut and paste.
fn bubble_sort(numbers: &mut Vec<i32>) {
let mut sorted = true;
for i in 0..numbers.len() {
sorted = true;
for j in 0..numbers.len() - 1 {
if numbers[j] > numbers[j + 1] {
numbers.swap(j, j + 1);
sorted = false;
}
}
}
if sorted {
break;
}
}
Merge Sort
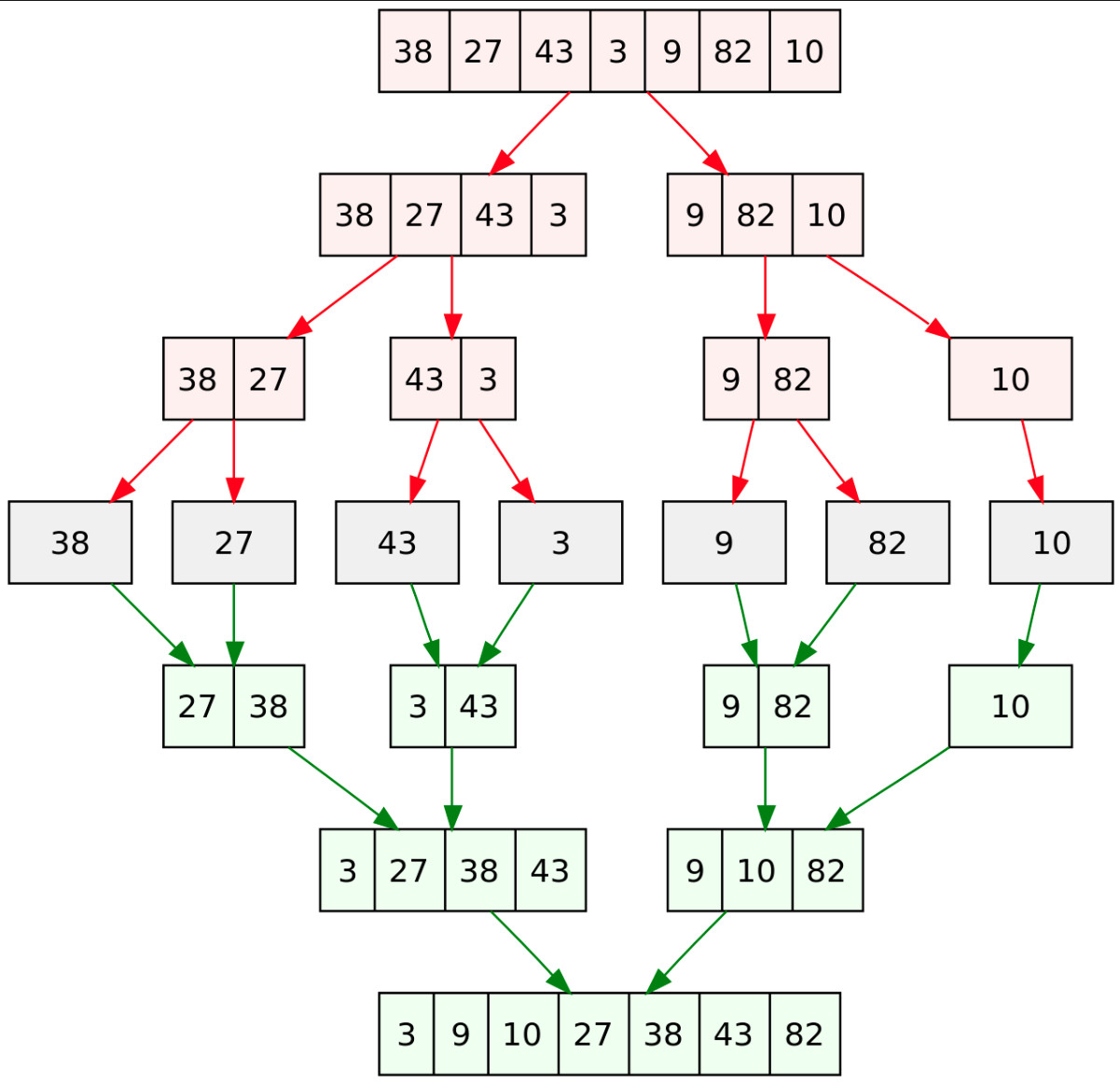
This is more interesting. This is known as a divide and conquer approach as we break the problem up. For this we need to
- Break the array in half until each level is 1 or 2 numbers (4 levels in this picture)
- Create empty array of original length
- Take element either from left of right depending on which is the largest
fn merge_sort(arr: &mut [i32]) -> Vec<i32> {
// Base case
if arr.len() > 1 {
// Split the array into two, left and right
let mid = arr.len() / 2;
let left_merge = merge_sort(&mut arr[..mid]);
let right_merge = merge_sort(&mut arr[mid..]);
let mut left_index = 0;
let mut right_index = 0;
for val in &mut *arr {
// Determine if left or right index is next
if right_index == right_merge.len() || (left_index < left_merge.len() && left_merge[left_index] < right_merge[right_index]) {
// Set left index as next value
*val = left_merge[left_index];
left_index += 1;
} else {
// Set right index as next value
*val = right_merge[right_index];
right_index += 1;
}
}
}
arr.to_vec()
}
fn main() {
let mut merge_numbers = vec![38, 27, 43, 3, 9,82, 10];
let answer4 = merge_sort(&mut merge_numbers);
println!("This is the answer {:?}", answer4);
}
Quick Sort
A similar approach to sorting but this time we
- Selection of the Pivot Element: The first step in the QuickSort algorithm is choosing a pivot element from the array. This can be any element from the array.
- Partitioning: The array is partitioned or reordered so that all elements less than the pivot come before the pivot, while all elements greater than the pivot come after it. After this step, the pivot is in its final position.
- Recursive Sort: The steps above are recursively applied to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values.
Here is the approach from co pilot
fn quick_sort(array: &mut [i32]) -> Vec<i32> {
let length = array.len();
if length <= 1 {
return array.to_vec();
}
let pivot = array[length - 1];
let mut left = 0;
let mut right = length - 1;
while left < right {
while array[left] < pivot {
left += 1;
}
while array[right] > pivot {
if right == 0 {
break;
}
right -= 1;
}
if left < right {
array.swap(left, right);
}
}
let mut left_sorted = quick_sort(&mut array[..left]);
let mut right_sorted = quick_sort(&mut array[left..]);
left_sorted.append(&mut right_sorted);
left_sorted
}
The solution by the course was this.
fn quick_sort_2(arr: &mut [i32], start: usize, end: usize) -> Vec<i32> {
if start < end {
// Partition function to return the pivot index
let mut i = start;
for j in start..end {
if arr[j] < arr[end] {
arr.swap(i, j);
i += 1;
}
}
arr.swap(i, end);
let p = i;
quick_sort_2(arr, start, p - 1);
quick_sort_2(arr, p + 1, end);
}
arr.to_vec()
}